ORIGINAL ARTICLE

 

Digital Spectrum Sensing Technique implemented on FPGA devices for Digital Television Applications

 

Técnica de detección de espectro digital implementada en dispositivos FPGA para aplicaciones de televisión digital

 

 

Mélany Gutierrez Hernández^I, Jorge Torres Gómez^I, Elias A. Perdomo Hourné^II

^IDepartment of Telecommunications and Telematics, Technological University of Havana (CUJAE), Cuba.

^IIDepartment of Automation and Computing System, Technological University of Havana (CUJAE), Cuba.

 

 

---

ABSTRACT

The rapid growth of wireless technology demands to employ the available spectrum efficiently. In this work, an Energy Detector is designed to be used in a Cognitive Radio scenario using a platform based on Software Defined Radio principles. The design of this detector is developed by using Simulink and Xilinx System Generator MATLAB software to be implemented on a Field Programmable Gate Array (FPGA) device. To sense the spectrum, the energy detector (ED) is the most used approach due to its low computational complexity. Furthermore, ED offers the ability to identify spectrum holes without prior knowledge regarding transmission characteristics of primary users. However, setting a threshold for energy detection requires to estimate noise power, which can be established by appropriate estimation methods. In this regard, a new method is proposed and implemented on FPGA to establish a threshold and detect properly the available spectrum. Results obtained reveal a proper performance of the proposed detector given by P_d>0.9 and P_fa=0.1, respectively, in the SNR range [-8, 15] dB. On the other hand, Digital Television in Cuba requires a robust and efficient automatic signal detection method to identify Television white spaces. Cognitive radio users would use these spectral holes to increase bandwidth and improve connectivity for wireless communications applications. To this end, this work is aimed to detect white spaces of the Digital Television spectrum using energy detector method. Simulation results show that the detector performs correctly on this scenario.

Key words: Spectrum Sensing, Cognitive Radio, Energy Detector, Noise Estimation, FPGA, Digital Television.

---

RESUMEN

El rápido crecimiento de la tecnología inalámbrica demanda emplear eficientemente el espectro disponible. En este trabajo se diseña un detector de energía para ser usado en un escenario de Radio Cognitivo utilizando una plataforma de Radio Definido por Software. El diseño de este detector es desarrollado empleando los softwares: Simulink y Xilinx System Generator de MATLAB para ser implementado en un dispositivo de tipo Arreglo de Compuertas Programables por Campo (FPGA). Para sensar el espectro, la detección de energía es el método de sensado más utilizado debido a su baja complejidad computacional. Además, el detector de energía ofrece la capacidad de identificar espacios disponibles en el espectro sin requerir un conocimiento previo de las características de transmisión de los usuarios primarios. Sin embargo, establecer un umbral para la detección de energía requiere el conocimiento de la potencia de ruido del canal, que puede ser establecida por métodos de estimación apropiados. En este sentido, un nuevo método es propuesto e implementado en FPGA para establecer el umbral y detectar correctamente la presencia de señales en el espectro. Los resultados obtenidos revelan el satisfactorio desempeño del detector propuesto dado por P_d>0.9 y P_fa=0.1 para relaciones señal a ruido bajas en el rango [-8, 15] dB. Por otro lado, en el caso de la televisión digital en Cuba se requiere un método robusto y eficiente de detección automático de señales que permita identificar los espacios en blanco de las bandas de televisión. Los usuarios cognitivos pueden utilizar estos espacios en blanco para aumentar y mejorar la conectividad en aplicaciones de comunicaciones inalámbricas. Con este fin, este trabajo tiene como objetivo detectar los espacios en blanco en el espectro de Televisión Digital usando la técnica de detección de energía. Los resultados de simulación demuestran que el detector propuesto posee un correcto comportamiento para este escenario.

Palabras claves: Sensado de Espectro, Radio Cognitivo, Detector de Energía, Estimación de Ruido, FPGA, Televisión Digital.

---

 

 

1. INTRODUCTION

The rapid grow in demand of new telecommunication services, supported by the miniaturization of computing devices, have intensely increased spectrum demand for wireless communications technologies. Wireless communications have several applications in modern life, as they allow users to access data networks, television services and videoconferences on real time. In this regard, users are to experience mobile communications at any place, any time as demanded on 5G (1). On the other hand, radio spectrum is a limited resource and therefore it is necessary to be used in an efficient manner. This is due to the shortage presented on available frequencies to insert new services and to extend the existing ones (2).

Recently, it have been reported that some frequency bands remain free most of the time, while others exhibits high congestion (3). In this sense, the static allocation of frequency bands represents an inefficient employment of the spectrum. Thus, Cognitive Radio (CR) emerges as an alternative to improve the use of the radio spectrum using dynamic assignment policy (4). CR paradigm allows secondary users to reuse unused bands of primary users. In this case, the available spectrum can be used by a variety of systems such as Cellular and Smart Electrical Networks where higher response rates are demanded in real time environments (5).

One of the main components of cognitive systems is provided by Spectrum Sensing (SS) techniques. This component enables to sense the activity on the radio spectrum where CR operates. Several detection methods have been developed depending on the available prior information, complexity and precision (6). Reported main methods for SS are: energy detection (ED) (7), matched filter (8) and cyclostationary features detection (9). These methods are reported to be used in a variety of applications such as Radio, Digital and Analog Television Systems (5).

ED technique represents the most common solution for heterogeneous wireless communication systems. In this approach, the wireless device estimates the radio frequency energy on the input signal to determine channel availability. This method offers major advantages in terms of low complexity and ease of implementation. ED does not need prior knowledge on the signal parameters, however, to establish a decision threshold it is necessary to estimate channel noise variance (10).

On the other hand, a variety of noise variance estimation techniques are reported, those available to integrate with the energy detector. For instance, the Rank Order Filtering (ROF) (11), Maximum Likelihood (ML) (12), Non Data Aided (NDA) Signal-to-Noise Ratio SNR estimator (13), Finite Difference Operator (14) and Maximize Geometric Mean (MGM) (15). Some of these estimation techniques demand for prior knowledge on main signal parameters, thus limiting their use on blind scenarios. This is the case of ML,NDA and Finite Difference Operator techniques. MGM and ROF solutions are difficult to implement due to prohibitive hardware complexity when a digital design is considered.

Currently, some developments have been conducted on spectrum sensing solutions for Digital Television (DTV) bands. In this regard, spectrum detection methods based on Pseudo Noise random sequence Autocorrelation (PNAC) on frame headers is proposed on (16). Although this method is simple to be implemented, has limited performance on low SNR regions. Report (17) proposes detection methods based on Cross-Correlation of the Pseudo-random sequence (PNCC) to improve probability of detection. Nevertheless, PNCC suffers from poor performance on channels of multiple-path fading.

DTV might provide large area coverage and represents a popular candidate for CR applications (18). DTV can be implemented according to various standards, among which are Advanced Television Systems Committee (ATSC), Digital Video Broadcasting-Terrestrial (DVB-T), Integrated Services Digital Broadcasting-Terrestrial (ISDB-T) and Digital Terrestrial Multimedia Broadcast (DTMB). Among these standards, DTMB is used in Cuba to provide DTV services.

Since the migration of Digital Television service has not been finished in Cuba, Analogue Television will coexist with Digital Television on the next few years. To efficiently reuse television white spaces (TVWS), it is necessary to implement digital and analog signal detection prototypes (18). Access to these TVWS benefits the deployment of wireless services. To this end, this work is aimed to detect TVWS on Digital Television spectrum using the ED. The proposal is based on its low complexity and ease of implementation. To this end, the current article addresses the design of ED method together with a novel noise estimation technique on FPGA.

The organization of the paper is as follows. In Section 2, the ED fundamentals are described and the proposed method to estimate channel noise power is explained in Section 3. FPGA implementation of the proposed method is addressed in Section 4 and performance of the proposed spectrum sensing method is demonstrated via MATLAB simulations in Section 5. Finally, our conclusions are presented in Section 6.

 

2. ENERGY DETECTOR

Energy detector (ED) has been vastly analyzed, and its performance has been evaluated under multiple communication channels (2). Improvements to this Spectrum Sensing method have also been reported for both local and cooperative sensing (19,20). Its major advantage is to allow broadband detection achieved by a low cost computational methods (21).

Depending on the occupied or inactive state of primary user, on a noisy channel, the detection of the signal of interest can be modeled by a binary hypothesis. The hypothesis H₀ is assumed when there is only noise in the channel, while the hypothesis H₁ is assumed when signal is corrupted by noise:

(1)

where r[n] is the received signal, s[n] represents the signal of interest transmitted by primary users and w[n] symbolizes the Additive White Gaussian Noise (AWGN) with zero mean and varianceN₀⁄2.

Fig. 1 shows the conventional energy detector block diagram. The signal is squared to obtain energy measurements. Then an average procedure is performed in time, where the output is called the test statistic Y. This output Y is then compared to the energy threshold. When the test statistic value Y is greater than the threshold λ, the presence of the primary user is declared, otherwise the primary user is considered to be absent.

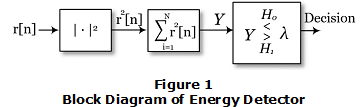
The energy detector performance can be evaluated by two performance metrics: probability of false alarm P_ƒa probability of detection P_d. False alarm happens when detector outputs H₁ and the channels condition is on H_0. In this scenario, the secondary user does not use the available spectrum and the opportunity to transmit is lost. Therefore, lower probabilities of false alarm give greater throughput of secondary users. The probability of false alarm is defined by (22):

(2)

where P_r (detected signal│H₀) is the probability to detect signal under the hypothesis H₀, λ symbolizes the detection threshold and ƒ(Y│H₀) represents the probability density function of the test statistic Y under the hypothesis H₀.

The probability of detection is defined as the probability to have the right decision when signals of interest is on the channel. In case of failure detection, the user starts unwanted secondary transmissions, causing interference to licensed user. This probability is defined by:

(3)

where P_r (detected signal│H₁) is the probability to detect signal under the hypothesis H₁ and ƒ(Y│H₁) represents the probability density function of the test statistic Y under the hypothesis H₁.

On both cases, the function ƒ(Y│H_i), i=0, 1 in (2) and (3) can be approximated by using the Central Limit Theorem (CLT) (23). In this work, received samples are normalized by noise variance, which in turn yields to following equations:

(4)

(5)

where is the Gaussian complementary distribution function,  is the number of samples observed in T seconds for a signal of bandwidth W, where N=WT and γ=σ_s²/σ_w² is the signal-to-noise ratio (SNR), where σ_w² and σ_s² are the channel noise power and signal power, respectively. For a given false alarm probability P_ƒa the threshold can be calculated according to Neyman-Pearson criterion by using (24):

(6)

The energy detection decision metric is, in principle, the energy of the received signal: . However, there is a considerable ambiguity in the definition of the test statistic by this measurement method. Some reports on this direction are based on the normalized energy of the received samples: (25,26). Other investigations states the normalization by the noise variance as (27,28):

(7)

where σ_w² is the noise variance and r[n] represents the input signal on the current development.

Equation (7) above is the test statistic chosen on the current solution. This formula allows to establish a fixed threshold without considering noise power values. This is the most reported formula to implement ED. However, equation in (7) demands to estimate channel noise power (σ_w²) to implement the decision block in Fig.1. Thus, in order to achieve automatic operation of the energy detector, it is necessary to implement a robust estimator of noise variance. Next Section is devoted to describe the proposed noise estimation technique.

 

3. PROPOSED METHOD TO ESTIMATE CHANNEL NOISE POWER

A variety of solutions is reported to estimate noise variance as described in [11-14]. Most of this solutions demands prior knowledge on main signal parameters and involve high complexity of operations. These solutions are limited to apply in practice on CR scenarios, where blind communication is established and multiple bands are analyzed. Additionally, their estimation error is not worthless and may affect the energy detection process.

To overcome the above limitations, a newnon-parametric approach to estimate noise variance is proposedin this work. The proposed method performs a simple processing method through the signal periodogram. By assuming that 90% of the frequency response area, provided by the signal periodogram, represents signal of interest, then the remainder 10% is assumed to be noise. Following this approach, next steps on the frequency domain comprise the method:

1. Power Spectral Density estimation: This is obtained by using the periodogram method (29):

(8)

where v[n]=r[n]π[n], 0≤n≤N-1, r[n] represents the signal of interest and π[n] represents the rectangular window.

2. Welch-Bartlett periodogram (29): The Welch-Bartlett periodogram is used to better estimate the Power Spectral Density from the received signal by averaging K times the expression in (8) as:

(9)

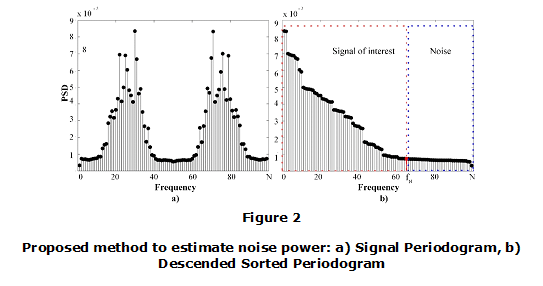
To illustrate, Fig. 2a) depicts the Welch-Bartlett periodogram of a given signal when K=10.

3. Ordering: The Welch periodogram obtained in step 2) is sorted from higher to lower values as shown in Fig. 2b) using the Bubble Sort Method. This method can be implemented using the following code:

 

Although the Bubble Sort Method seems to be complex and time demanding, this is implemented in parallel on FPGA and final cost in hardware does not represent a major concern. This is discussed into next Sections.

4. Noise power estimation: Based on the graph of Fig. 2b), the 90% of the frequency response area is assumed to be the signal of interest while the other 10% is assumed to be noise. The total area is determined by computing the Trapezoids Method as:

(10)

• Next, the total area is multiplied by 0.9 in order to find a level to represent the 90%. Formula in (10) is applied to the periodogram in Fig. 2b) by setting a=0 after incrementing the value of h sequentially on a variety of frequency steps. These partial areas are sequentially compared to the 90 % level of the total area to find the limit ƒ_N after which noise samples are only present. This is depicted by the right box on Fig. 2b).

• Finally, noise power is estimated by averaging noise samples inside the right box on Fig. 2b) as

(11)

where represents the total number of samples, ƒ_Nis the number of frequency samples after which only noise is present and represents the noise sequence samples inside the right box on Fig. 2b).

 

4. FPGA IMPLEMENTATION OF THE PROPOSED METHOD

The ED method is based on the flow diagram shown in Fig. 3. Based on this scheme, some parameters are modified from the conventional diagram in Fig. 1. The test statistic, at the output of the detector, is the result of normalizing the energy of the received signal by the noise variance value. In this solution, noise variance parameter is estimated in accordance with proposed method described on the previous Section.

Current work describes an FPGA design based on the scheme depicted in Fig. 3. A variety of advantages such as the increaseof processing speed and flexibility are provided by digital technology. In addition, FPGA enables to implement parallel structures and the increase in execution speed, comparable to powerful General Purpose Processors. The system is implemented in Xilinx FPGA, supported by the Xilinx System Generator (XSG) tool. This tool is integrated with the mathematical assistant MATLAB, on Simulink platform.

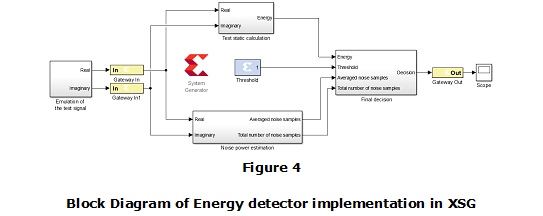
The design of the proposed energy detector is divided into four stages: Emulation of the test signal, Noise power estimation, Test static calculation and Final decision. As depicted in Fig. 4, the output of the emulated test signal stage is divided into real and imaginary parts. These parts are inputs of next two parallel stages: Test static calculation and Noise power estimation. The outputs of these two stages are then compared to the predefined threshold in the final decision stage to detect whether the signal of interest is present or not. Emulation of the test signal stage is created in the MATLAB Simulink scenario without FPGA design. The other three stages are implemented in XSG for FPGA devices. These three stages are separated from Simulink blocks by the Gateways In and Gateway Out blocks to comprise the entity ports.

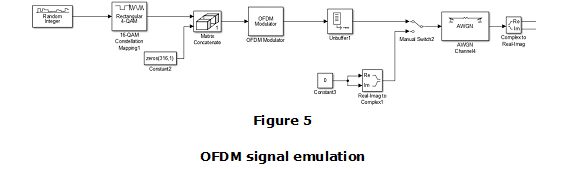
The first stage is the Emulation of the test signal block, which is implemented by Simulink blocks only, not on FPGA, to provide a testing signal to establish detector performance. In this case, an OFDM waveform is employed similar to the used on DTV signals as depicted in Fig. 5. Main parameters as symbol rate and length are settled in accordance with DTMB standard. These values are defined on Section of Results. Firstly, a random signal is generated and modulated using Quadrature Amplitude Modulation (QAM). Then, an OFDM modulator block is employed to build the signal of interest. Then, Gaussian white noise is added to the signal as the channel model. For illustration purposes,the implemented DTV signal was not conformed by some parameters as error correction and header sequence.

To implement the second stage, Noise power estimation, the 90% method discussed in the previous section is used. Its implementation is divided into 4 stages in which the XSG library blocks are connected as follows:

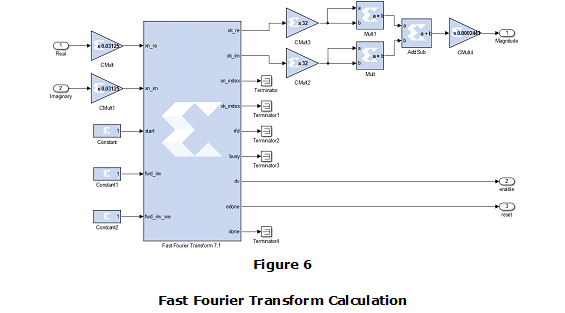
1. Compute the Discrete Fourier Transform of the input signal using the Fast Fourier Transform (FFT) 7.1 block of the XSG library, as depicted in Fig. 6. The inputs of this system are real and imaginary parts of the test signal. CMult blocks are used to normalize real and imaginary inputs. The start input is kept active in '1' for the entire time interval because the FFT selected mode operates continuously. Outputs of this block are provided by determining the real (xk_re) and imaginary (xk_im) parts of the FFT procedure, as well as data valid (dv) and edone signals. By means of xk_re and xk_im signals, frequency magnitude signal can be determined. This is done using the XSG Mult and AddSub blocks to square both the real and the imaginary part and then add them together. In addition, this value is normalized between the total number of samples using Cmult4. Data valid (dv) and edone signals are used on next stages as enabling and reset pulses, respectively.

2. Perform the Welch periodogram averaging multiple periodograms. XSG does not provide any block to implement this functionality. In this situation, the operation was designed in hardware description language (HDL). This code is added to the Simulink platform using the Black Box block from XSG. The inputs of this block are Magnitude and enable outputs from Fig. 6. Welch periodogram is performed with a variable window size to be configured according to the needs of the design. In this work, a window of 32 samples was used. To implement Welch periodogram, serial samples at the input was first transformed into parallel samples, that was also performed in HDL code. The pseudo code of this stage is reported in Algorithm 2.

3. Ordering: This non-linear operation is not available on XSG and is also designed on HDL. The ordering process is implemented using the Bubble Sort Method as described in previous section. Algorithm 3 describes this ordering process, which is synthetized in parallel by the ISE compiler. Thus, the sorting procedure is implemented just in one clock period. Finally, the ordered samples are converted from parallel to serial to properly connect with next XSG blocks. The serialization process was then implemented in HDL as well.

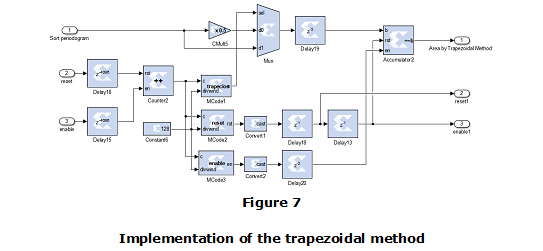
4. Compute the area of sorted values at stage 3 before by the Trapezoids Method using blocks: Accumulator, Mux, Counter,CMult and Mcode, as depicted on Fig. 7. The Mcode1 block is used to allow the inclusion of some MATLAB statements to halve first and last samples on equation (10). The multiplexor allows the selection of first and last samples as selected by the output of Mcode1 block. This two samples are multiplied using CMult5 times 0.5 and then all the samples are accumulated together with Accumulator2 block. These operations implement equation (10) at the output signal 1 on Fig. 7. Output signals 2 and 3 are used to reset and enable next stage.

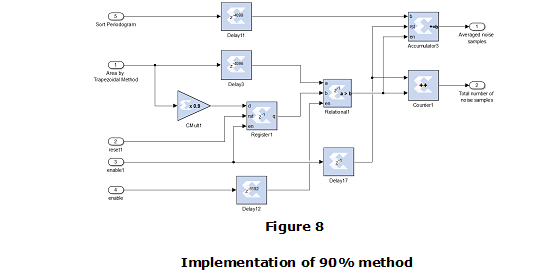
• Multiply by 0.9 the area obtained in stage 4 to establish the 90% level of the total area as implemented by the multiplier CMult1 in Fig. 8. Then, based on the sorted periodogram obtained by Algorithm 3, the area is computed sequentially by using the same scheme depicted on Fig. 7. In this case, the partial results are delayed by  samples using block Delay3 as shown in Fig. 8. Finally, each obtained value at the input of Relational1 block is compared to the 90% level obtained at the output of Cmult1 block, as shown in Fig. 8. Output of Relational1 block enables to average proper vector noise samples.

• To avoid the use of a divider block, the value of variable  in equation (11) is considered on the final stage as an equivalent multiplier to decrement hardware complexity. This is further analyzed on next paragraphs.

Stages above implement the Noise power estimation block in Fig. 4. Then, Test static calculation block in Fig. 4 was implemented by using XSG blocks to determine the energy of the simulated signal. Firstly, the real and imaginary parts of the signal are raised to the square by using blocks Mult5 and Mult4 as depicted in Fig. 9. Then, all values are accumulated by the Accumulator1 block to compute the signal energy. The output of Accumulator1 must be delayed by  samples as seen in Fig. 9. This is due to the processing delay of the noise power estimation stage given by the parallelization process and the implementation of the proposed method.

In the Final decision block in Fig. 4 the comparison between the test statistic and threshold value is performed as described in (7). By using this expression together with (11), an equivalent expression to the test statistic may be determined by:

(12)

after rearranging the dividing terms in (7). In this new equivalent expression in (12), dividers are avoided and the implementation is equivalent. Equation in (12) is implemented in Fig. 9 by connecting, multiplying and comparing properly the outputs of Fig. 8 and energy calculated in Fig. 9. The energy signal obtained in Acumulator1 is multiplied using Mult3 with the total number of noise samples offered by output 2 in Fig. 8. Then, after multiplying the average noise values times the threshold by using CMult6 block, this is compared to the output of Mult3 to provide a final decision.

 

5. RESULTS AND DISCUSION

To analyze performance of proposed detector, the Receiver Operational Characteristic (ROC curve) is examined in comparison to ideal ED where noise variance match exactly to that on the channel. To this end, an OFDM waveform is employed, similar to the used on DTV signals by employing the scheme in Fig. 5. Main parameters as bandwidth of nominal channel by B=6MHz and the number of subcarriers by 3780 are settled in accordance with DTMB used in the International Telecommunications Union (ITU) region 2 (Americas).The used sampling frequency is four times the bandwidth ƒ_m=4B. Fig. 10 shows the increasing probability of detection related to the increase of false alarm probability. Fig. 10 a) and b) depicts results for SNR equals to -7 dB and -8 dB, respectively. The detector performs correctly, as alleged IEEE standard, and similar to ideal ED.

In order to analyze how the total number of samples influence the effectiveness of the estimator, the simulation of the detector implemented in XSG with a BPSK signal was made. The signal bandwidth is given by ƒ_s= 0.5kHz and the used sampling frequency is ten times the bandwidth ƒ_m=10ƒ_s. Fig. 11 shows values of probability of detection, these values increase with the increment of the total number of samples. Obtained results are similar to the ideal detector. In addition, Fig. 12 exhibits results by means of a variety of signals like Quadrature Amplitude Modulation (QAM), already mentioned BPSK and Orthogonal Frequency-Division Multiplexing (OFDM with QAM to emulate television signal). Considering values of Fig. 12, the implemented solutions performs correctly by processing other modulation type formats. In comparison with the ideal ED, performance detection is almost the same.

To compare with other reported solutions, the analysis of the proposed noise estimator performance is presented in terms of absolute error and in Normalized-mean-square-error (NMSE). Considering the estimated noise variance (), the absolute error on the noise estimated value is given by:

(13)

where σ_w² represents the exact noise power at the channel. Fig. 13 demonstrates a minimal error on noise estimation using the proposed method comparing with (14). The NMSE is calculated by:

(14)

where M is the independent number of simulation data. Fig. 14 shows a small error using NMSE characteristic, which is higher in comparison with the result obtained by NDA (13). In the other hand, NDA requires prior knowledge of the signal, while the proposed method in this work is completely blind to all the signal parameters.

In order to evaluate performance for a variety of SNR values, Fig. 15 shows the detection probability by using the OFDM signal obtained by the scheme in Fig. 5. In comparison with the ideal ED, detection performance is almost similar for SNR values superior to -8 dB.

Hardware complexity on FPGA of the proposed method is analyzed by the Resource Estimator block, presented on Xilinx library. Fig. 16 shows the results obtained using this block. The necessary resources for implementation on FPGA are just a few, in correspondence with the simplicity of the ED (30).

 

6. CONCLUSIONS

In this work, a blind sensing method for spectrum sensing based on energy detection technique in Xilinx System Generator for FPGAs has been implemented. The proposed design applies directly to implement the sensing component of Cognitive Radio devices. Also, this method allows the detection of primary users without prior knowledge on signal parameters.

The proposed solution is valuable, considering the trade-off between implementation complexity and precision, since the algorithm is efficient and the complexity is comparable to other reported. In addition, real-time application is affordable due to the implemented solution on FPGA.

The proposed final solution allows to estimate noise levels in bands where signal and noise are mixed. Additionally, this estimation is integrated to the energy detector to use on spectrum sensing applications. Future work on this direction demands to validate the proposed solution in a hardware co-simulation environment.

Results obtained demonstrate the applicability of the energy detection method for a variety of signals. Especially, the application of the proposed solution to Digital Television signals provides proper results based on DTMB standard used in Cuba. In this sense, using this solution it is possible to detect digital television white spaces to be reused for wireless communications purposes.

 

7. REFERENCES

1. Calabuig J, Monserrat JF, Gómez-Barquero D. 5th generation mobile networks: A new opportunity for the convergence of mobile broadband and broadcast services. IEEE Commun Mag. 2015 Feb;53(2):198–205.

2. Satheesh A, H AS, G LS, Sagar S, M HK. Spectrum sensing techniques A comparison between energy detector and cyclostationarity detector. In: 2013 International Conference on Control Communication and Computing (ICCC). 2013. p. 388–93.

3. Abdulsattar, Mahmood A, Hussein, Zahir A. Energy detection technique for spectrum sensing in cognitive radio: a survey. Int J Comput Netw Commun. 2012;4(5):223.

4. Nguyen TT, Nguyen TM, Nguyen HV, Dang KL. Hardware implementation of reception diversity techniques for spectrum sensing efficiency enhancement in cognitive radio network. In: 2013 Third World Congress on Information and Communication Technologies (WICT 2013). 2013. p. 69–73.

5. Khan AA, Rehmani MH, Reisslein M. Cognitive Radio for Smart Grids: Survey of Architectures, Spectrum Sensing Mechanisms, and Networking Protocols. IEEE Commun Surv Tutor. 2016 Firstquarter;18(1):860–98.

6. Sardar M, Karthikeyan KV. Study on sensing techniques for cognitive radio network: A survey. In: 2016 International Conference on Circuit, Power and Computing Technologies (ICCPCT). 2016. p. 1–7.

7. Umar R, Sheikh AUH, Deriche M. Unveiling the Hidden Assumptions of Energy Detector Based Spectrum Sensing for Cognitive Radios. IEEE Commun Surv Tutor. 2014 Second;16(2):713–28.

8. Sklar B, Ray PK. Digital Communications: Fundamentals and Applications. 2nd ed. Pearson; 2014.

9. Badawy A, Khattab T. A novel peak search amp; save cyclostationary feature detection algorithm. In: 2014 IEEE Wireless Communications and Networking Conference (WCNC). 2014. p. 253–8.

10. Hu X, Xie X-Z, Song T, Lei W. An algorithm for energy detection based on noise variance estimation under noise uncertainty. In: 2012 IEEE 14th International Conference on Communication Technology (ICCT). 2012. p. 1345–9.

11. Sequeira S, Mahajan RR, Spasojevic P. On the noise power estimation in the presence of the signal for energy-based sensing. In: 2012 35th IEEE Sarnoff Symposium (SARNOFF). 2012. p. 1–5.

12. Farahiyah D, Nguyen TT, Kaiser T. Noise power estimation with DVB-T input for spectrum sensing in cognitive radio network. In: 2016 2nd International Conference on Wireless and Telematics (ICWT). 2016. p. 92–6.

13. Socheleau FX, Aissa-El-Bey A, Houcke S. Non data-aided SNR estimation of OFDM signals. IEEE Commun Lett. 2008 Nov;12(11):813–5.

14. Martínez DM, Andrade ÁG. Reducing the effects of the noise uncertainty in energy detectors for cognitive radio networks. Int J Commun Syst [Internet]. 2014 Dec 4 [cited 2017 Mar 27]; Available from: https://www.growkudos.com/publications/10.1002%252Fdac.2907

15. Wang K, Zhang X. Robust spectrum sensing algorithm for cognitive radio networks. In: IEEE 10th INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING PROCEEDINGS. 2010. p. 1520–3.

16. Chen HS, Gao W, Daut DG. Spectrum Sensing for DMB-T Systems Using PN Frame Headers. In: 2008 IEEE International Conference on Communications. 2008. p. 4889–93.

17. Xu A, Shi Q, Yang Z, Peng K, Song J. Spectrum Sensing for DTMB System Based on PN Cross-Correlation. In: 2010 IEEE International Conference on Communications. 2010. p. 1–5.

18. Luo Z, Wang J, Pan C, Zhu J, Li X. A weighted cooperative spectrum sensing method based on double-threshold credibility in DTMB systems. In: 2015 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting. 2015. p. 1–6.

19. Bkassiny M, Jayaweera SK, Li Y, Avery KA. Blind cyclostationary feature detection based spectrum sensing for autonomous self-learning cognitive radios. In: 2012 IEEE International Conference on Communications (ICC). 2012. p. 1507–11.

20. Chen Y. Improved energy detector for random signals in gaussian noise. IEEE Trans Wirel Commun. 2010 Feb;9(2):558–63.

21. Bagwari A, Tomar GS. Multiple Energy Detection vs Cyclostationary Feature Detection Spectrum Sensing Technique. In: 2014 Fourth International Conference on Communication Systems and Network Technologies. 2014. p. 178–81.

22. Liu C, Li M, Jin ML. Blind Energy-based Detection for Spatial Spectrum Sensing. IEEE Wirel Commun Lett. 2015 Feb;4(1):98–101.

23. Song J, Feng Z, Zhang P, Liu Z. Spectrum sensing in cognitive radios based on enhanced energy detector. IET Commun. 2012 May;6(8):805–9.

24. Chairman Martin. In the Matter of Unlicensed Operation in the TV Broadcast Bands, Additional Spectrum for Unlicensed Devices Below 900 MHz and in the 3 GHz Band. 2008 Nov. Report No.: FCC 08-260.

25. Nuñez WA, Bañacia AS. Simulation and FPGA implementation of television white space sensing using energy detection for cognitive radio. In: 2015 International Conference on Humanoid, Nanotechnology, Information Technology,Communication and Control, Environment and Management (HNICEM). 2015. p. 1–6.

26. Chaitanya GV, Rajalakshmi P, Desai UB. Real time hardware implementable spectrum sensor for Cognitive Radio applications. In: 2012 International Conference on Signal Processing and Communications (SPCOM). 2012. p. 1–5.

27. Urkowitz H. Energy detection of unknown deterministic signals. Proc IEEE. 1967 Apr;55(4):523–31.

28. Stasionis L, Serackis A. A new approach for spectrum sensing in wideband. In: Eurocon 2013. 2013. p. 125–32.

29. Dimitris G. Manolakis, Vinay K. Ingle, Stephen M. Kogon. Statistical and Adaptive Signal Processing. Spectral Estimation, Signal Modeling, Adaptive Filtering, and Array Processing. Artech House; 2005.

30. Sabat SL, Srinu S, Kumar NK, Udgata SK. FPGA realization of spectrum sensing techniques for cognitive radio network. In: 2010 International Workshop on Cognitive Radio (IWCR). 2010. p. 1–5.

 

 

Received: 22/11/2017

Approved: 8/5/2018

 

 

Mélany Gutierrez Hernández, BSc in Telecommunications and Electronics Engineering, Affiliation: Department of Telecommunications and Telematics, Technological University of Havana (CUJAE), Cuba. She is currently working on developing software applications in the field of cognitive radio systems. Emails: [e-mail]; [e-mail].