My SciELO
Services on Demand
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Cuban Journal of Agricultural Science
On-line version ISSN 2079-3480
Cuban J. Agric. Sci. vol.50 no.1 Mayabeque Jan.-Mar. 2016
Cuban Journal of Agricultural Science, 50(1): 25-38, 2016, ISSN: 2079-3480
ORIGINAL ARTICLE
Validation of a mathematical model developed for the solid state fermentation process of the sugar cane (Saccharum officinarum) with sweet potato (Ipomoea batata Lam)
Validación de un modelo matemático desarrollado para el proceso de fermentación en estado sólido de la caña de azúcar (Saccharum officinarum) con boniato (Ipomoea batata Lam)
Dailyn Sosa,I J.C. Dustet,II R. Boucourt,I Zoraya Rodríguez,I
IInstituto de Ciencia Animal, Apartado Postal 24, San José de las Lajas, Mayabeque.
IIGrupo de Biotecnología Aplicada, Facultad de Ingeniería Química, Instituto Superior Politécnico José Antonio Echeverría, La Habana.
ABSTRACT
The objective of this research was to validate the mathematical model developed by Sosa et al. (2012) with the experimental data of the solid state fermentation of the sugar cane with sweet potato. This model took into account the mass and energy balances, the logistic equation for microbial growth and an auxiliary equation for the specific growth rate in function of temperature. Sensitivity analysis of the model main variables responses was conducted. It was verify that the parameters which affect predictions in a range of ± 30% variation were the substrate apparent density, the biomass/oxygen yield and the initial inoculum concentration. The heat capacity, thermal conductivity, porosity, biomass/substrate, biomass/water yields and higher biomass concentration did not cause variations in the results. The mathematical model allowed determining the total fermentation time and the time in which is necessary to turn the substrate to get a more efficient process.
Key words: solid fermentation, mathematic modeling, animal feed.
RESUMEN
El objetivo de este estudio fue validar el modelo matemático desarrollado por Sosa et al. (2012) con los datos experimentales de la fermentación en estado sólido de la caña de azúcar con boniato. Este modelo tuvo en cuenta los balances de masa y energía, la ecuación logística para el crecimiento microbiano y una ecuación auxiliar para la velocidad específica de crecimiento en función de la temperatura. Se realizó el análisis de sensibilidad de las principales variables respuestas del modelo. Se constató que los parámetros que afectaron las predicciones en un intervalo de ± 30 % de variación fueron la densidad aparente del sustrato, el rendimiento biomasa/oxígeno y la concentración inicial de inóculo. La capacidad calorífica, conductividad térmica, porosidad, rendimientos biomasa/sustrato, biomasa/agua y concentración máxima de biomasa no provocaron variaciones en los resultados. El modelo matemático permitió determinar el tiempo total de fermentación y el tiempo en que es necesario voltear el sustrato para lograr un proceso más eficiente.
Palabras clave: fermentación sólida, modelación matemática, alimento animal.
INTRODUCTION
In Cuba there is great interest in producing animal feed from agro-industrial waste. The Instituto de Ciencia Animal (ICA) has technologies for the obtaining of different products, among them: Saccharina, Sacchamaize, Sacchasorghum and Sacchasweet potato. The latter is obtained from the solid state fermentation (SSF) of sugar cane with sweet potato and can be used in the non-conventional feeding of monogastric animals (Rodriguez et al. 1998). The most acceptable technology for obtaining Sacchasweet potato was to perform fermentation in rustic conditions, which consist on a solids bed extended on a flat surface, exposed to the environment, without circulation of forced aeration.
The rustic fermentations can be an alternative for animal feed production, due to the bioreactors do not have application in this type of process because of its higher investment and operating costs. However, in the rustic SSF are some difficulties because the main environmental variables are not possible to control. Hence, it is necessary to develop mathematical models which allow to describe physical phenomena that take place and to establish operation conditions.
In the current scientific literature are available numerous papers on mathematical modeling for SSF, which are conducted under controlled bioreactors conditions, which is an important tool in the simulation of these processes (Valiño et al. 2011). This does not happen equally to the rustic SSF, since they have no models to characterize the process.
The most of models developed for bioreactors establish operating strategies that improve the SSF yield (Mitchell et al. 2010), although very few were validated, optimized and allowed to scale the process satisfactorily (Julian et al. 2014). Generally, these models allow solving the problems of heat and mass transfer, as well as significantly reducing the number of experiments, which in turn saves time and resources (Hasan et al. 2007, Singhania et al. 2009 and Mitchell et al. 2010).
From this perspective, Sosa et al. (2012) developed a mathematical model for rustic SSF that took into account the mass and energy balances. The objective of this research was to validate the mathematical model developed by these authors with experimental data from the fermentation of sugar cane with sweet potato under floor conditions.
MATERIALS AND METHODS
Inoculum preparation. An activated culture from the LRO (Rhodotorula) strain was used, belonging to the microorganisms collection of the Departamento de Ciencias Biofisiológicas, of Instituto de Ciencia Animal. This yeast was culture in malt extract media (pH 8), it was incubated in orbital shaker at 110 rpm and 29 °C of temperature. Samples of 400 mL of this culture were taken and put into a fermenter containing 40 L of a mdeia (table 1) designed to guarantee the microorganisms conditions. A discontinuous fermentation at 26 °C during 20 h was carried out.

Solid state fermentation of sugar cane with sweet potato. Clean sugar cane was used, between 24 and 48 h after the cut and sweet potato after 24 h of the harvest. They were ground in a stationary Bolgar mill and mixed in the 50:50 (w/w) proportion. Minerals salts 0.5 % (w/w) and urea 1 % (w/w) was added. Plots of 1 m2 were prepared, with solids bedding heights of 0.10 and 0.15 m (Rodriguez 2004), inoculated by sprinkling at 48h with a yeast culture at a concentration of 5.63•106 live cells•mL-1. The inoculum size represented 10 % of the substrate initial weight. The samplings were carried out at 0, 24, 48, 72 and 96 h in five points of the plot, to determine the dry matter according to AOAC (1995). The temperature was measured with digital sensor (Digi-Termo 10 °C-110 °C) previously to the sampling. Mean temperature was 26 °C. All experimental data taken at sampling points were averaged to form a single value of each parcel.
Mathematical model. The phenomenological model proposed by Sosa et al. (2012) was used, which took into account the description of the physical situation in mathematical terms. The model consists on the following equations:
Kinetic equation:

X- biomass concentration (kg of biomass/kg of substrate)
Xm- maximum concentration (kg of biomass/kg of substrate)
Xo– initial concentration of biomass respectively (kg of biomass/kg of substrate),
μ – the specific growth rate (h-1) and t is the time (h)
Energy balance:
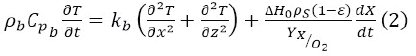
ρb - bedding density in the solids (kg/m3)
Cpb- heat capacity of bedding in the solids (J/kg °C)
T - temperature (ºC)
t - time (h)
kb - thermal conductivity of bedding in the solids
(J/mh°C),
x - bedding length in the solids (m)
z - bedding height in the solids (m)
∆H0 - standard combustion heat of organic molecules (J/kg of oxygen)
ρS - substrate density (kg/m3)
ε - bedding porosity in the solids (-)
X - biomass concentration (kg of biomass/kg of substrate)
YX⁄O2 - yield coefficient of biomass/oxygen (kg of biomass/kg of oxygen).
Mass balances:
Substrate:

Oxigen:

Water:

Where:
CS - solids concentration (kg/m3)
εes - bedding porosity in the solids (-)
t - time (h)
ρS – substrate density (kg/m3)
YX⁄S – yield coefficient of biomass/substrate (kg of biomass/kg of substrate)
X - biomass concentration (kg of biomass/kg de substrate)
CO2 – oxygen concentration (kg/m3)
YX⁄O2- yield coefficient of biomass/oxygen (kg of biomass/kg of oxygen)
CH2O - water concentration (kg/m3)
Yx/H2O - yield coefficient of biomass/water (kg of biomass/kg of water)
Auxiliary equation:

Where:
μ– specific growth rate (h-1)
A - empirical constant (h-1)
B - empirical constant (-)
Ea1 – activation energy (J/g mol)
Ea2 – non -activation energy (J/g mol)
R - universal gas constant (J/g mol K)
T -temperature (ºC)
The kinetics equation is used to determine the biomass production during the process. The energy balance allow to determine the temperature profiles, while mass balances allow to determine the rate of substrate and oxygen intake and the water production rate, respectively. The auxiliary equation represents the variations of the specific growth rate, depending on the temperature.
In this research the solution and validation of the mathematical model was developed, as well as its applications. All these aspects are in correspondence with the strategy described by Mitchell et al. (2006) for the development of mathematical models in the fermentative processes.
Estimation of physical properties. The determination of physical properties is an essential aspect for the mathematical modeling of these processes. In this article a compilation of the parameters taken into account to validate the mathematical model from the data reported in the literature (table 2) was performed.
To determine the density and thermal conductivity of the bedding in the solids, the equations of Ali and Mahmoodzadeh (2009) were used, which allowed treat the system as pseudo-homogeneous:
ρb=ερa+(1-ε) ρs (7)
kb=εka+(1-ε) ks (8)
ρa – air density (kg/m3)
ka - termical conductivity of the air (J/mh°C)
ks - termical conductivity of the substrate (J/mh°C).
While for the heat capacity it was worked with the equation reported by Sangsurasak and Mitchell (1995):
Cpb = εCpa+(1-ε) Cps (9) where:
Cpa - heat capacity of the air (J/kg°C)
Cps -heat capacity of the substrate (J/kg°C)
The sensitivity analysis of the response variables (temperature, substrate intake rate and water production rate) was performed depending on the physical properties, kinetic and transport, for what it was worked in a range of ± 30% of the reference value of each parameter. The fermentation time was 24 h.
Model solution. The solution of the partial differential equation, which represents the energy balance, was obtained by the finite differences method, while for mass balances were not required the use of numerical methods, because there were determined intake rates and main compounds production. All equations were programmed in MATLAB software, version 7.8.0.347 (2009), which provides results in matrix form. In addition, the following initial and contour conditions for the solution of the model were taken into account:
Initial condition:
t=0 T=Ta
Boundary conditions:
x=0 T=Ta
x=1 m T=Ta
z=0 T=Ta
z=0.15 m T=Ta
where:
Ta - mean temperature
Model validation was made from the same initial conditions of the experimental work. Values of temperature and humidity content were also taken in five points of the matrix, which were averaged to obtain a single value. These results were compared with the experimental study.
RESULTS AND DISCUSSION
Validation of the matemathical modelefficiency.Energy balance. Figure 1 shows the temperature profile obtained by the model and the experimental results of the rustic SSF of sugar cane with sweet potatoes. In addition it provides that the proposed model predicted, satisfactorily, the experimental data. The observed differences could be given by the variations in the variables that affect the models predictions.
Figure 2 shows the modeling results, for 10 and
15 cm of bedding height in the solids. For 15 cm higher temperature values were reached, which coincides with Rodriguez et al. (2006) studies for this type of fermentation process.
The bedding height in the solids is one of the main factors to control in fermentations performed under rustic conditions. As the height is higher, higher temperatures will be found, mainly, due, to the high thermal isolation capacity of the substrate, which prevents the metabolic heat dissipation generated during fermentation (Rodriguez et al. 2006).
In the SSF processes, mainly in those performed under rustic conditions, in which the main parameters are not controlled, important amounts of metabolic heat are generated. This produces higher temperature gradients that may favor by the non-inclusion of forced aeration in the processes with bioreactors or because the substrate cannot turn, as happen under rustic conditions (Carrasco et al. 1997). Other aspects which can affect are the low thermal conductivity of biological materials and the humidity content of the substrate (Rodriguez et al. 2006). The temperature profiles are directly related to the microbial kinetics, because as the cells population grows the metabolic heat is generated. In figure 2 is observed that these maintained a similar performance to the microbial growth which the logistic equation describes.
Figure 3 shows the estimated performance of the specific growth rate, biomass formation, the rate of substrate and oxygen intake as well as the water production rate for 24 h of fermentation. During the first 13 h of the process, the specific growth rate remained, approximately, constant. From this moment increased, and then decreased (figure 3a).The decrease in microbial growth should be understood, mainly, to the high temperatures reached during the fermentation process (figure 2). In the area where the highest values of specific growth rate were recorded, the appropriate interval temperature for microorganisms growth was obtained, which in this case ranged between 30-40 ° C, approximately.
Figure 3b shows that during the first hours of fermentation there is biomass formation, although in lower proportion because of the low growth rates that were showed. The same occurs with the substrate and oxygen intake rates, as well as with the water production rate that, in this range were very low (figure 3c). As increased the specific growth rate of the microorganisms from 13h, the highest nutrients intake were obtained, as well as higher biomass concentrations and water production (figure 3).
In the processes of solid state fermentation (SSF), biomass formation and oxygen intake represent the most convenient way to verify the microbial growth. In these aerobic systems, the heat metabolic generation rate is proportional to the oxygen intake rate (Mitchell et al. 2006), while the aeration in the rustic SSF is related to the bedding height. As the latter is smaller, better aeration in the system is achieved. For higher bedding heights, aeration does not satisfy the metabolic heat extraction and then it is needed to turn the substrate.
A comparison between the dry matter values offered by the model and those obtained from the experimental procedure are shown in figure 4. As seen, the results are in function of the bedding height in the solids. It was found that the highest differences are 10 cm. This is due to variations which may exist in those parameters that affect the mathematical model. Moreover, the dry matter was higher when the bedding height in the solids was increased, because in this case the fermentation process is not as efficient, because there is lower oxygenation, higher metabolic heat accumulation and then, higher temperatures which limit microbial growth are reached. These results coincide with studies carried out by Carrasco et al. (1997) for fermentations with sugar cane, in which was also demonstrated that, when turning the substrate, the dry matter increased due to the loss of solid humidity.
Sensitivity analysis. The sensitivity analysis showed that the variables which affect the predictions of the mathematical model were the substrate apparent density, the biomass/oxygen yield and the initial inoculums concentration. While the heat capacity, thermal conductivity, porosity, biomass/substrate and biomass/water yields and the higher biomass concentration did not cause variations in the results.
The results of the variables which affect the model predictions are shown in figure 5. In all cases, there were no affectations in the value of maximum temperature reached during the process. Differences resided in the time needed to reached and were up to 10 °C approximately with respect to the reference value for the same period of fermentation, which is of great interest because this is one of the factors that most influences on the microbial growth. From the practical point of view, these differences are the most important, they offer an idea of the need to experimentally measure the variables that affect the rustic SSF. In addition, they bring problems in selecting the appropriate time to turn the substrate.
In previous studies, Sangsurasak and Mitchell (1998) developed a mathematical model in two-dimensional space for a packed- bed bioreactor. They found that one of the variables that affect the model predictions was the initial inoculum concentration, while with respect to the substrate apparent density, they explain that there was not much clarity on how it can affect microbial growth, because if this is limited by the available surface area of the substrate, then this variable would have little effect.
When the biomass/oxygen yield decreases, the metabolic heat increases and variations in the temperature profile are obtained (figure 5c). The yields depend on the biomass reduction degree and energy yields of the process (Erickson et al. 1978). Generally, the stoichiometric parameters considerably vary, due to the substrates diversity used in the SSF and therefore, also change the reduction degrees. This means that the yields may be different from a fermentation process to another.
Table 3 shows the results of the sensitivity analysis for variables that did not affect the mathematical model predictions. This was carried out for a time of 15 h because it was when there was a higher difference. In this regard, Smits et al. (1999) offered similar results for the heat capacity. In addition, the fact that the thermal conductivity did not cause changes in the results indicates that the conduction mechanism was not affected by the changes in this transport parameter. In the case of the porosity, the few variations constitute an advantage for rustic SSF, since there were not affectations in the development of the process after turn the bedding in the solids, which is essential, since this is the only way in which it is achieve to control the temperature in these processes.
One of the main practical applications of the mathematical model in study is to determine the time in which the substrate should be move due to high temperatures. From the results of the equations of mass and energy balances, it can state that between 13-15 h of fermentation higher microorganisms growth rate occur, thereby the rate of substrate and oxygen intake increase, as well as the water production rate. This demonstrates an important metabolic activity in the optimum temperature range for growth (30 - 40 °C).
When values over this range were reached, it is necessary to turn the substrate, since the growth specific rate begins to decrease because of the high temperatures that occur in the system, due to the low metabolic heat dissipation generated. A study of the fermentation time performance for various bedding heights in the solids and different biomass/oxygen yields is show in figure 6. As can be seen, as the bedding height in the solids increases, the time in which the substrate should turn decreases up to a value that remained constant, despite height continue increasing. The time was reduced when decreasing the biomass/oxygen yield. The arrow on the graph indicates the fermentation time in which the optimum temperature range (30 - 40 °C) for growth was reached, from which the substrate must be moved in this study.
From the practical point of view, these results are indispensable for the fermentations performed under rustic conditions, then turning the substrate is the most effective way to control the temperature in this type of process. From the graph it can also determine, the time required for fermentation, which will depend on whether or not reach the protein and fiber percentages suitable for animal feed.
It is concluded that the mathematical model developed by Sosa et al. (2012) was able to predict the experimental results from the fermentation of sugar cane with sweet potato.
In addition, an adequate description of the rustic SSF process in two dimensions of space and time was achieved. With the model it can predict important operating variables, such as the time at which to turn the substrate and the maximum height of the bedding in the solids to maintain an appropriate temperature value in the process.
The parameters that affect the predictions of the mathematical model were the substrate apparent density, the biomass/oxygen yield and the initial inoculum concentration. The remaining variables did not cause changes in the results. Generally, the model can be applied in studies of solid state rustic fermentations used in animal feed production.
REFERENCES
Ali, F. M. & Mahmoodzadeh, V. B. 2009. ‘‘Modeling of temperature gradients in packed-bed solid-state bioreactors’’. Chemical Engineering and Processing: Process Intensification, 48 (1), pp. 446–451, ISSN: 0255-2701, DOI: 10.1016/j.cep.2008.06.001.
AOAC. 1995. Official methods of analysis of AOAC. 16th ed., vol. 1, Washington, D.C.: AOAC International, ISBN: 978-0-935584-54-7, Available: <http://www.cabdirect.org/abstracts/19951414840.html>, [Accessed: February 16, 2016].
Carrasco, E., Bocourt, R. & Elías, A. 1997. ‘‘Layer height and tumbling on sugar cane fermentation with bovine faeces’’. Cuban Journal of Agricultural Science, 31 (1), p. 43, ISSN: 2079-3480.
Erickson, L. E., Selga, S. E. & Viesturs, U. E. 1978. ‘‘Application of mass and energy balance regularities to product formation’’. Biotechnology and Bioengineering, 20 (10), pp. 1623–1638, ISSN: 1097-0290, DOI: 10.1002/bit.260201009.
Hasan, S. A., Kumar, S. & Kumar, S. 2007. ‘‘Modelling of a packed bed solid-state fermentation bioreactor using the N-tanks in series approach’’. Biochemical Engineering Journal, 35 (1), pp. 20–28, ISSN: 1369-703X, DOI: 10.1016/j.bej.2006.12.016.
Hasan, S. D. M., Costa, J. A. V. & Sanzo, A. V. L. 1998. ‘‘Heat transfer simulation of solid state fermentation in a packed-bed bioreactor’’. Biotechnology Techniques, 12 (10), pp. 787–791, ISSN: 0951-208X, 1573-6784, DOI: 10.1023/A:1008887828569.
Himmelblau, D. M. 1982. Basic principles and calculations in chemical engineering. Englewood Cliffs, NJ, United States: Prentice-Hall, Inc., Available: <http://www.osti.gov/scitech/biblio/5410794>, [Accessed: February 16, 2016].
Julián, R. M. C., Ramos, S. L. B. & Gómez, A. A. O. 2015. ‘‘Modelación matemática del proceso de enriquecimiento proteico del bagazo de caña de azúcar en un biorreactor de lecho fijo’’. Tecnología Química, 34 (3), pp. 207–216, ISSN: 2224-6185.
MathWorks, Inc. 2009. MATLAB®. version 7.8.0.347, [Microsoft Windows], Available: <https://www.mathworks.com> .
Mitchell, D. A., Cunha, L. E. N., Machado, A. V. L., de Lima Luz Jr., L. F. & Krieger, N. 2010. ‘‘A model-based investigation of the potential advantages of multi-layer packed beds in solid-state fermentation’’. Biochemical Engineering Journal, 48 (2), pp. 195–203, ISSN: 1369-703X, DOI: 10.1016/j.bej.2009.10.008.
Mitchell, D. A. & von Meien, O. F. 2000. ‘‘Mathematical modeling as a tool to investigate the design and operation of the zymotis packed-bed bioreactor for solid-state fermentation’’. Biotechnology and Bioengineering, 68 (2), pp. 127–135, ISSN: 1097-0290, DOI: 10.1002/(SICI)1097-0290(20000420)68:2<127::AID-BIT1>3.0.CO;2-K.
Mitchell, D. D. A., Berovič, P. M. & Krieger, D. N. 2006. ‘‘Solid-State Fermentation Bioreactor Fundamentals: Introduction and Overview’’. In: Mitchell, D. D. A., Berovič, D. M. & Krieger, D. N. (eds.), Solid-State Fermentation Bioreactors, Springer Berlin Heidelberg, pp. 1–12, ISBN: 978-3-540-31285-7, Available: <http://link.springer.com/chapter/10.1007/3-540-31286-2_1>, [Accessed: February 16, 2016].
Perry, R. H., Green, D. W. & Maloney, J. O. 1984. Perry’s Chemical engineers’ handbook. 6th ed., New York: McGraw-Hill, ISBN: 978-0-07-049479-4.
Rodríguez, A. Z. 2004. Uso del boniato en la tecnología de fermentación en estado sólido de la caña de azúcar. Ph. D. thesis, Universidad Agraria de La Habana ‘Fructuoso Rodríguez Pérez’, La Habana, Cuba.
Rodríguez, Z., Boucourt, R., Elías, A., Herrera, F. R. & Nuñez, O. 2006. ‘‘Effect of layer height on the fermentation dynamics of sugarcane (Saccharum officinarum) and sweet potato (Ipomea batata Lam) mixtures’’. Cuban Journal of Agricultural Science, 40 (2), pp. 161–170, ISSN: 2079-3480.
Rodríguez, Z., Elías, A. & Riverí, Z. 1998. ‘‘Studies on theutilization of sweet potato (Ipomea batata Lam) in solidstate fermentation of sugar cane’’. Cuban Journal of Agricultural Science, 32 (3), pp. 285–290, ISSN: 2079-3480.
Sangsurasak, P. & Mitchell, D. A. 1995. ‘‘Incorporation of death kinetics into a 2-dimensional dynamic heat transfer model for solid state fermentation’’. Journal of Chemical Technology & Biotechnology, 64 (3), pp. 253–260, ISSN: 1097-4660, DOI: 10.1002/jctb.280640307.
Sangsurasak, P. & Mitchell, D. A. 1998. ‘‘Validation of a model describing two-dimensional heat transfer during solid-state fermentation in packed bed bioreactors’’. Biotechnology and Bioengineering, 60 (6), pp. 739–749, ISSN: 1097-0290, DOI: 10.1002/(SICI)1097-0290(19981220)60:6<739::AID-BIT10>3.0.CO;2-U.
Saucedo, C. G., Gutiérrez, R. M., Bacquet, G., Raimbault, M. & Viniegra, G. G. 1990. ‘‘Heat transfer simulation in solid substrate fermentation’’. Biotechnology and Bioengineering, 35 (8), pp. 802–808, ISSN: 1097-0290, DOI: 10.1002/bit.260350808.
Singhania, R. R., Patel, A. K., Soccol, C. R. & Pandey, A. 2009. ‘‘Recent advances in solid-state fermentation’’. Biochemical Engineering Journal, 44 (1), pp. 13–18, ISSN: 1369-703X, DOI: 10.1016/j.bej.2008.10.019.
Smits, J. P., Sonsbeek, H. M. van, Tramper, J., Knol, W., Geelhoed, W., Peeters, M. & Rinzema, A. 1999. ‘‘Modelling fungal solid-state fermentation: the role of inactivation kinetics’’. Bioprocess Engineering, 20 (5), pp. 391–404, ISSN: 0178-515X, 1615-7605, DOI: 10.1007/s004490050607.
Sosa, D., Boucourt, R. & Dustet, J. C. 2012. ‘‘Use of mathematical modeling on the solid-state fermentation processes of fibrous substrates for animal feeding’’. Cuban Journal of Agricultural Science, 46 (2), pp. 119–126, ISSN: 2079-3480.
Valiño, E. C., Ibarra, A., García, Y., Izquierdo, E. & Dustet, J. C. 2011. ‘‘Descripción de la fermentación del bagazo de caña por Trichoderma viride M5-2 en un biorreactor estático mediante un modelo fenomenológico’’. Cuban Journal of Agricultural Science, 45 (3), p. 267, ISSN: 2079-3480.
Weber, F. J., Tramper, J. & Rinzema, A. 1999. ‘‘A simplified material and energy balance approach for process development and scale-up of Coniothyrium minitans conidia production by solid-state cultivation in a packed-bed reactor’’. Biotechnology and Bioengineering, 65 (4), pp. 447–458, ISSN: 1097-0290, DOI: 10.1002/(SICI)1097-0290(19991120)65:4<447::AID-BIT9>3.0.CO;2-K.
Received: June 3, 2015
Accepted: March 25, 2016
Dailyn Sosa, Instituto de Ciencia Animal, Apartado Postal 24, San José de las Lajas, Mayabeque. Email: dsosa@ica.co.cu














