My SciELO
Services on Demand
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista Cubana de Ciencias Informáticas
On-line version ISSN 2227-1899
Rev cuba cienc informat vol.11 no.2 La Habana Apr.-June 2017
ARTÍCULO ORIGINAL
Reducción de ruido en imágenes basada en las dependencias inter-escala e intra-escala entre los coeficientes wavelets
Image denoising using interscale and intrascale dependencies between wavelet coefficients
Rafael Arturo Trujillo Codorníu1*, Yanet Cesaire Velázquez 2, Antonio Cedeño Pozo 3
1 Facultad de Ing. Eléctrica, Universidad de Oriente, Ave. Patricio Lumumba s/n Altos de Quintero, Santiago de Cuba, Cuba. CP.:90500, rtrujillo@edistancia.uo.edu.cu
2 DeSoft, Santiago de Cuba, Cuba, yanet.cesaire@scu.desoft.cu
3 Facultad 5. Universidad de las Ciencias Informáticas, Carretera a San Antonio de los Baños, km 2 ½, Torrens, Boyeros, La Habana, Cuba. CP.: 19370, acedeno@uci.cu
*Autor para la correspondencia: rtrujillo@edistancia.uo.edu.cu
RESUMEN
En el presente trabajo se analizan los métodos de reducción de ruido en imágenes basados solamente en la correlación intra-escala e inter-escala de los coeficientes wavelet. Se presenta además un novedoso esquema de umbralización wavelet espacialmente adaptativo que incorpora información de los coeficientes vecinos. Las pruebas experimentales muestran que el método propuesto es consistentemente superior a otros métodos del estado del arte que explotan la dependencia intra-escala e incluso ligeramente superior a BiShrink que utiliza la correlación inter-escala.
Palabras clave: umbralización wavelet; reducción de ruido en imágenes; dependencia inter-escala; dependencia intra-escala.
ABSTRACT
In this paper, image denoising methods, based only on the interscale and intrascale dependencies between wavelet coefficients, are analyzed. In addition, a novel thresholding scheme for spatially adaptive wavelet denoising is presented. The scheme incorporates information from the neighboring coefficients. Experimental results show that the proposed method is consistently superior to others state-of-the-art methods based on intrascale dependencies, and even slightly better than BiShrink which uses the inter-scale correlation.
Key words: wavelet thresholding; image denoising; interscale dependencies; intrascale dependencies
INTRODUCCIÓN
Durante la adquisición y trasmisión de las imágenes estas son frecuentemente contaminadas por el ruido. El tipo y la energía del ruido dependen de la forma en que las imágenes han sido capturadas, pero generalmente la mayor parte de este proviene de las fluctuaciones en el número de fotones que arriba al sensor de la cámara y, adicionalmente, al ruido térmico de los dispositivos electrónicos y de los conversores análogo-digitales. Como regla, el ruido puede ser bien modelado como ruido aditivo gaussiano blanco. La reducción del ruido es sumamente importante ya que, en el análisis de imágenes, la extracción de la información útil puede ser significativamente perturbada por la presencia del mismo.
En la Figura 1, por ejemplo, (tomada de (Luisier 2010)) se muestra como el ruido altera los resultados de un detector de bordes en una imagen de resonancia magnética nuclear. Para lidiar con este fenómeno es necesario realizar un pre-procesamiento de la imagen que trate de disminuir los niveles de ruido manteniendo sus características esenciales.
Tradicionalmente, para la reducción del ruido, se han utilizado filtros lineales tales como el filtro de Wiener. Sin embargo, en los últimos 20 años, a partir de los trabajos de Donoho (Donoho and Johnstone, 1993) el foco de atención se ha movido hacia métodos no lineales basados en la transformada wavelet discreta (DWT).
Para aplicar estos métodos a imágenes se necesita utilizar la transformada wavelet bidimensional (2D). La transformada multidimensional se construye típicamente aplicando la transformada wavelet 1D independientemente a lo largo de cada dimensión del conjunto de datos, produciendo un número de sub-bandas. En el caso bidimensional esta descomposición diádica de la DWT se muestra en la Figura 2. La matriz de datos original B0 (o imagen) es descompuesta en 4 sub-bandas B1, H1, V1 y D1, resultantes de aplicar la DWT a cada fila y luego a cada columna. El conjunto B1 contiene una imagen suavizada de la imagen original mientras que H1, V1 y D1 contienen los detalles (que reflejan cambios abruptos en la intensidad de un pixel de la imagen a otro adyacente). Cada sub-banda es de un cuarto del tamaño de la imagen original. Luego, la banda de aproximación B1 puede ser transformada para obtener B2 y detalles adicionales H2, V2 y D2 donde los subíndices reflejan el nivel de la transformación. A su vez es posible transformar B2 y así sucesivamente.
La reducción de ruido basada en la DWT involucra tres pasos básicos, que son: descomposición en sub-bandas wavelets de la imagen con ruido a través de la DWT, modificación de los coeficientes wavelets obtenidos y reconstrucción de la imagen a partir de los coeficientes modificados mediante la transformada inversa. La modificación de los coeficientes wavelets se hace usualmente a través de la umbralización que consiste en comparar el coeficiente con un umbral dado y hacerlo cero (declararlo “insignificante”) si su magnitud es menor que el umbral. Si la magnitud del coeficiente es mayor que el umbral el coeficiente se considera significativo y se modifica en dependencia de la regla de umbralización. De esta manera, el umbral distingue los coeficientes insignificantes posiblemente originados por el ruido de aquellos coeficientes significativos que son generados por las estructuras importantes de la imagen. Como el ruido gaussiano es promediado y consecuentemente reducido en gran medida en las bandas Bi, la umbralización se ejecuta sólo en las bandas de detalle.
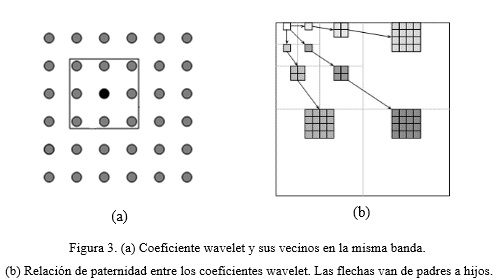
En los métodos originales de reducción de ruido (Donoho y Johnstone, 1993) los coeficientes wavelets eran umbralizados término a término en base a su magnitud individual. Investigaciones posteriores (por ejemplo, Cai y Silverman, 2001), han mostrado que se obtienen mejores resultados si se considera la correlación que tienen las magnitudes de los coeficientes. En efecto, aunque los coeficientes wavelets de una imagen no tienen correlación unos con otros, si tienen determinada correlación sus magnitudes. Liu y Moulin (Liu y Moulin , 2001), en particular, muestran que las dependencias más significativas son las correlaciones intra-escala que aparecen entre la magnitud del coeficiente wavelet y la magnitud de los coeficientes de una vecindad del mismo en la misma escala (Figura 3a) y las correlaciones inter-escala que aparecen entre la magnitud del coeficiente wavelet y la magnitud del coeficiente padre (Figura 3b), que se encuentra en la misma localización espacial pero en la siguiente banda de descomposición.
Experimentalmente se ha demostrado, por ejemplo, que los coeficientes vecinos de un coeficiente wavelet significativo son, con relativa alta probabilidad, significativos también (Cai y Silverman, 2001). Cai y Silverman propusieron dos esquemas diferentes de umbralización, que consideran esta correlación espacial, llamados NeighBlock y NeighCoeff. Chen et al., (2005), aplicaron NeighCoeff a la reducción de ruido en imágenes y lo renombraron como NeighShrink. Esquemas ligeramente mejorados de este método se proponen en (Biswas y Om, 2016). El método NeighShrink toma en cuenta la magnitud del coeficiente y de sus inmediatos vecinos para determinar si el mismo es significativo o no. Los resultados experimentales demostraron que NeighShrink ofrece mejores resultados que el filtrado de Wiener y que los otros métodos clásicos de umbralización wavelet: VisuShrink y SUREShrink (Donoho y Johnstone, 1995). NeighShrink ha sido aplicado, además, a ruidos no aditivos (ver Vanithamani y Umamaheswari, 2014). En (Yang y Wei, 2012) y (Yang et al, 2014) se propone un esquema tipo NeighShrink (que llamaremos NeighPreserve) en el que la magnitud de los coeficientes, que se decide contienen información de la imagen, es preservada. Para tomar la decisión de hacer cero o preservar el coeficiente se usa la magnitud del mismo y la de sus inmediatos vecinos.
Entre los métodos que toman en cuenta la correlación inter-escala el más significativo es el introducido en (Sendur y Selesnick, 2002). En este trabajo se introduce una regla de umbralización bivariada (denominada en lo adelante BiShrink) que toma en cuenta las magnitudes del coeficiente y del coeficiente padre para la umbralización.
Estos métodos pueden ser mejorados determinando algunos parámetros de los mismos, para cada sub-banda, de manera independiente, de forma tal que se minimice el estimador insesgado del riesgo de Stein (SURE), (ver Luisier, 2010 y Lihong et al, 2014). Por ejemplo, en (Dengwen y Wengang, 2008) y (Sabahaldin y Gorashi, 2012) se perfecciona el método NeighShrink determinando el umbral óptimo y la cantidad de vecinos a considerar para cada sub-banda, sin embargo, ya esto introduce un esquema de optimización que no se relaciona directamente con las correlaciones entre los coeficientes wavelets que es el objeto del presente artículo.
El método BiShrink, que se basa en las correlaciones inter-escala, es consistentemente superior a NeighShrink y a NeighPreserve en las imágenes patrón (Sendur y Selesnick, 2002). Este resultado es contradictorio pues, en efecto, Liu y Moulin (Liu y Moulin , 2001) establecen que la dependencia intra-escala (entre vecinos) es ligeramente más fuerte que la dependencia inter-escala (entre padres e hijos). Esto permite llegar a la conclusión de que ni NeighShrink ni NeighPreserve capturan en su totalidad la correlación intra-escala para la reducción del ruido.
En el presente trabajo se presenta un novedoso esquema de umbralización wavelet espacialmente adaptativo para la reducción del ruido en imágenes. El método propuesto está inspirado en el esquema general de Cho y Bui, (Cho y Bui, 2005), e incorpora información de los coeficientes vecinos. Las pruebas experimentales muestran que es consistentemente superior a NeighShrink y a NeighPreserve e incluso ligeramente superior a BiShrink con lo que se puede deducir que captura mucho mejor la dependencia intra-escala.
MATERIALES Y MÉTODOS
Como es conocido, una imagen en escala de grises puede ser representada mediante un arreglo bidimensional en el que el valor de cada elemento del arreglo representa la intensidad del pixel correspondiente. Así, asumiendo que la matriz f={fij} representa la imagen original y la matriz g={gij} la imagen ruidosa, se tiene:
![]()
donde ![]() representa una matriz de ruido blanco con distribución normal
representa una matriz de ruido blanco con distribución normal ![]() La supresión del ruido puede formularse como el problema de encontrar una estimación
La supresión del ruido puede formularse como el problema de encontrar una estimación ![]() de f={fij} a partir de la imagen con ruido g={gij} que minimice el error medio cuadrático:
de f={fij} a partir de la imagen con ruido g={gij} que minimice el error medio cuadrático:
![]()
Las imágenes a color o multiespectrales se pueden representar utilizando varios arreglos (uno para cada canal, por ejemplo: tres para las imágenes a color RGB) por lo que sin perder generalidad se puede limitar el análisis a las imágenes en escala de grises.
En el dominio wavelet, si usamos una transformada wavelet ortogonal W , obtenemos:
![]()
donde ![]() representan el coeficiente wavelet i,j en el nivel de descomposición k de la imagen degradada g={gij}, de la imagen original f={fij} y del ruido
representan el coeficiente wavelet i,j en el nivel de descomposición k de la imagen degradada g={gij}, de la imagen original f={fij} y del ruido ![]() respectivamente. De esta manera, en este dominio, el problema se transforma en hallar una estimación
respectivamente. De esta manera, en este dominio, el problema se transforma en hallar una estimación ![]() a partir de
a partir de ![]() que minimice el error medio cuadrático.
que minimice el error medio cuadrático.
Esquema de umbralización NeighShrink
En el método NeighShrink para cada coeficiente wavelet ![]() se necesita considerar una vecindad Vij del mismo. Esta vecindad se toma de manera que contenga el mismo número de píxeles por encima, por debajo, a la izquierda y a la derecha del pixel a considerar. Esto significa que los tamaños posibles de la vecindad Vij son 3x3, 5x5, 7x7, etc. En la Figura 3a se muestra una vecindad de 3x3 centrada en el coeficiente wavelet a considerar que es el tamaño de ventana más usado y que ofrece, como regla, mejores resultados. Sea
se necesita considerar una vecindad Vij del mismo. Esta vecindad se toma de manera que contenga el mismo número de píxeles por encima, por debajo, a la izquierda y a la derecha del pixel a considerar. Esto significa que los tamaños posibles de la vecindad Vij son 3x3, 5x5, 7x7, etc. En la Figura 3a se muestra una vecindad de 3x3 centrada en el coeficiente wavelet a considerar que es el tamaño de ventana más usado y que ofrece, como regla, mejores resultados. Sea
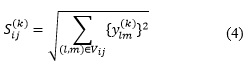
El valor de ![]() puede ser visto como un indicador que refleja en qué medida la zona de la imagen correspondiente al coeficiente
puede ser visto como un indicador que refleja en qué medida la zona de la imagen correspondiente al coeficiente ![]() presenta cambios bruscos de intensidad. Nótese que en la suma (4) se deben omitir aquellos términos que se salen de la sub-banda a analizar. La estimación
presenta cambios bruscos de intensidad. Nótese que en la suma (4) se deben omitir aquellos términos que se salen de la sub-banda a analizar. La estimación ![]() que realiza NeighShrink del coeficiente wavelet
que realiza NeighShrink del coeficiente wavelet ![]() se obtiene a partir de la siguiente expresión:
se obtiene a partir de la siguiente expresión:
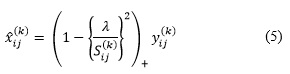
Donde como es usual ![]() es el umbral universal de Donoho. El umbral de Donoho requiere el conocimiento previo de la varianza del ruido
es el umbral universal de Donoho. El umbral de Donoho requiere el conocimiento previo de la varianza del ruido ![]() Si no se tiene un conocimiento “a priori” de esta varianza la misma puede ser calculada (ver, por ejemplo, Leigh et al., 2011), a partir de los coeficientes wavelets
Si no se tiene un conocimiento “a priori” de esta varianza la misma puede ser calculada (ver, por ejemplo, Leigh et al., 2011), a partir de los coeficientes wavelets ![]() de la banda D1, mediante el estimador:
de la banda D1, mediante el estimador:
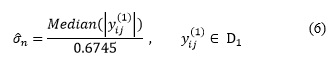
Esquema de umbralización NeighPreserve
El método NeighPreserve propuesto en (Yang y Wei, 2012) y (Yang et al, 2014) aplica la siguiente regla: Si las magnitudes de todos los coeficientes de la vecindad Vij son menores que el umbral de Donoho ![]() el coeficiente se hace cero, en caso contrario la estimación
el coeficiente se hace cero, en caso contrario la estimación ![]() que realiza este método es simplemente
que realiza este método es simplemente ![]() .
.
Esquema de umbralización BiShrink
Como se mencionó anteriormente el método BiShrink introducido en (Sendur y Selesnick, 2002) toma en cuenta las magnitudes del coeficiente a analizar y del coeficiente padre para la umbralización. Sea ![]() el coeficiente padre del coeficiente
el coeficiente padre del coeficiente ![]() . Entonces la regla de umbralización de este método es:
. Entonces la regla de umbralización de este método es:
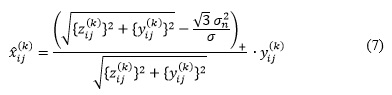
Este estimador requiere el conocimiento previo de la varianza del ruido ![]() y de la varianza marginal
y de la varianza marginal ![]() para cada coeficiente wavelet. La varianza del ruido puede evaluarse de acuerdo a la Ec. (6). Para estimar la varianza marginal se utilizan varianzas locales (Sendur y Selesnick, 2002). Este esquema se ha aplicado, en particular, para realzar las imágenes obtenidas por ultrasonido en la detección de tumores de seno (Wilson et al, 2015)
para cada coeficiente wavelet. La varianza del ruido puede evaluarse de acuerdo a la Ec. (6). Para estimar la varianza marginal se utilizan varianzas locales (Sendur y Selesnick, 2002). Este esquema se ha aplicado, en particular, para realzar las imágenes obtenidas por ultrasonido en la detección de tumores de seno (Wilson et al, 2015)
Esquema de umbralización propuesto
Las imágenes son altamente heterogéneas, típicamente contienen muchas regiones suaves intercaladas por contornos en los cuales hay cambios bruscos en la intensidad. En el dominio Wavelet esto se refleja en que una gran mayoría de los coeficientes wavelet en cada banda de detalle son pequeños y los restantes pueden ser de amplitud significativa. El histograma de los coeficientes wavelet de una banda se aleja del histograma de una distribución normal precisamente porque posee un pico pronunciado en el cero y colas más largas. Esto se modela bastante bien con distribuciones de Gauss generalizadas (ver, por ejemplo, Chang y Vetterli, 2000). En la mayoría de los trabajos se asume que los parámetros de la distribución son iguales para todos los coeficientes wavelets (o al menos iguales para los de una misma banda). En el método que se propone, para obtener una estrategia espacialmente adaptativa, asumiremos que cada coeficiente wavelet ![]() es una variable independiente con media cero que sigue una distribución de Gauss generalizada (GGD) cuyos parámetros, en especial la varianza, varían espacialmente. Para incluir la influencia de los coeficientes vecinos en la fórmula de umbralización se utilizó el esquema general propuesto por Cho y Bui, (Cho y Bui, 2005). Este esquema general modela la distribución multivariada del coeficiente wavelets a umbralizar con el resto de los coeficientes que se incluirán en la fórmula de umbralización. La distribución GGD propuesta por (Cho y Bui, 2005) es:
es una variable independiente con media cero que sigue una distribución de Gauss generalizada (GGD) cuyos parámetros, en especial la varianza, varían espacialmente. Para incluir la influencia de los coeficientes vecinos en la fórmula de umbralización se utilizó el esquema general propuesto por Cho y Bui, (Cho y Bui, 2005). Este esquema general modela la distribución multivariada del coeficiente wavelets a umbralizar con el resto de los coeficientes que se incluirán en la fórmula de umbralización. La distribución GGD propuesta por (Cho y Bui, 2005) es:
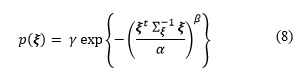
donde ![]() y
y ![]() son parámetros que determinan la forma de las superficies de equidensidad y
son parámetros que determinan la forma de las superficies de equidensidad y ![]() es una constante de normalización definida por
es una constante de normalización definida por ![]() ;
; ![]() y por la matriz de covarianza
y por la matriz de covarianza ![]() . Puede apreciarse que si
. Puede apreciarse que si ![]() = 2 se obtiene una distribución normal multivariada con media igual al vector nulo. Para determinados casos, de la distribución multivariada, se logran deducir fórmulas de umbralización óptimas utilizando métodos Bayesianos. En particular si
= 2 se obtiene una distribución normal multivariada con media igual al vector nulo. Para determinados casos, de la distribución multivariada, se logran deducir fórmulas de umbralización óptimas utilizando métodos Bayesianos. En particular si ![]() representa el vector bidimensional (x1 , x2) formado por el coeficiente wavelet bajo consideración x1 y su coeficiente padre x2 se obtiene una distribución multivariada de la cual se deriva el esquema de umbralización BiShrink (ver Cho y Bui, 2005).
representa el vector bidimensional (x1 , x2) formado por el coeficiente wavelet bajo consideración x1 y su coeficiente padre x2 se obtiene una distribución multivariada de la cual se deriva el esquema de umbralización BiShrink (ver Cho y Bui, 2005).
En el presente trabajo se aplica este mismo esquema sólo que en este caso se consideran el coeficiente wavelet y sus vecinos inmediatos. Para disminuir la dimensionalidad del modelo en lugar de considerar la distribución multivariada del coeficiente y sus vecinos se considera la distribución multivariada del coeficiente y la raíz cuadrada de la suma de los cuadrados de los vecinos ![]() , o sea, el vector
, o sea, el vector ![]() representaría en este caso el vector bidimensional (x1, N1). Igualmente se asume que
representaría en este caso el vector bidimensional (x1, N1). Igualmente se asume que ![]() . Estas simplificaciones permiten, utilizando las mismas técnicas de Cho y Bui, deducir una fórmula relativamente simple de umbralización.
. Estas simplificaciones permiten, utilizando las mismas técnicas de Cho y Bui, deducir una fórmula relativamente simple de umbralización.
Denotemos por ![]() la varianza del coeficiente
la varianza del coeficiente ![]() y mediante
y mediante ![]() la varianza del coeficiente
la varianza del coeficiente ![]() . Obsérvese que para simplificar la notación se omite el supra índice k. Obviamente se tiene
. Obsérvese que para simplificar la notación se omite el supra índice k. Obviamente se tiene ![]() . Entonces la umbralización que se propone es:
. Entonces la umbralización que se propone es:
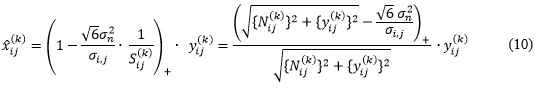
donde ![]() es la estimación del coeficiente
es la estimación del coeficiente ![]() ,
, ![]() es la varianza del ruido,
es la varianza del ruido, ![]() la varianza del coeficiente
la varianza del coeficiente ![]() y
y ![]() Puede apreciarse la semejanza de la expresión (10) con la fórmula de umbralización (7) de BiShrink. Esencialmente, al margen del cambio en alguna constante, se sustituye el coeficiente padre en (7) por la raíz cuadrada de la suma de los cuadrados de los vecinos del coeficiente a analizar.
Puede apreciarse la semejanza de la expresión (10) con la fórmula de umbralización (7) de BiShrink. Esencialmente, al margen del cambio en alguna constante, se sustituye el coeficiente padre en (7) por la raíz cuadrada de la suma de los cuadrados de los vecinos del coeficiente a analizar.
La varianza del ruido ![]() puede estimarse a partir de la Ec. (6), mientras, para estimar la varianza
puede estimarse a partir de la Ec. (6), mientras, para estimar la varianza ![]() del coeficiente
del coeficiente ![]() , se toma una vecindad Vij del coeficiente
, se toma una vecindad Vij del coeficiente ![]() . Asumiendo que la correlación entre las varianzas de los coeficientes
. Asumiendo que la correlación entre las varianzas de los coeficientes ![]() de la vecindad es alta tenemos que
de la vecindad es alta tenemos que ![]() para todo
para todo ![]() Por tanto una estimación de
Por tanto una estimación de ![]() puede obtenerse empíricamente como:
puede obtenerse empíricamente como:
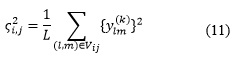
donde L es la cantidad de coeficientes contenidos en la vecindad Vij. Entonces ![]() puede estimarse como:
puede estimarse como:
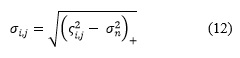
Los resultados experimentales indican que el tamaño óptimo de la vecindad, para la mayoría de las imágenes de prueba, es de 7x7, por lo que L= 49.
El algoritmo puede resumirse de la siguiente manera:
-
Transformar los datos al dominio wavelet a través de la transformada wavelet discreta.
-
Estimar la varianza del ruido usando la ecuación (6).
- Para cada sub-banda de detalle y para cada coeficiente wavelet
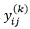 en la sub-banda:
en la sub-banda:
a) Estimar la varianza
usando la ecuación (11) a partir de una vecindad Vij de 7x7 coeficientes.
b) Estimar la varianza
mediante la ecuación (12).
c) Calcular
mediante la ecuación (4) utilizando una ventana de 3x3 coeficientes.
d) Estimar
(o sea, calcular
) utilizando
,
y
en la ecuación (10).
4. Obtener el estimado de la imagen f a través de la transformada wavelet inversa de los coeficientes ![]() .
.
RESULTADOS Y DISCUSIÓN
En las pruebas experimentales se compara el algoritmo propuesto con los algoritmos mencionados, específicamente con NeighShrink (Cai y Silverman, 2001; Chen et al., 2005), BiShrink (Sendur y Selesnick, 2002), y NeighPreserve (Yang y Wei, 2012). Veinte imágenes patrón (Figura 4), que se han convertido en estándares para la evaluación de algoritmos de reducción de ruido, se utilizan en las pruebas.
En la Tabla 1 se presentan los valores PSNR promedio obtenidos por cada método y en la Tabla 2 y Tabla 3 los valores PSNR de algunas de las imágenes utilizadas.
Los resultados de las Tablas ( Tabla 1, Tabla 2 y Tabla 3) muestran que el método NeighShrink ofrece resultados similares al método propuesto sólo cuando el nivel de ruido es bajo (![]() = 10 y
= 10 y ![]() = 20). A medida que el nivel de ruido aumenta la diferencia entre el método propuesto y el Neigh Shrink se hace apreciable llegando, como promedio, a 2 dB. El método NeighPreserve mejora, en algunas imágenes, a NeighShrink para niveles altos de ruido, pero no supera al método propuesto ni a BiShrink en ningún caso.
= 20). A medida que el nivel de ruido aumenta la diferencia entre el método propuesto y el Neigh Shrink se hace apreciable llegando, como promedio, a 2 dB. El método NeighPreserve mejora, en algunas imágenes, a NeighShrink para niveles altos de ruido, pero no supera al método propuesto ni a BiShrink en ningún caso.
En la Figura 5 se aprecian los resultados de cada método ante un ruido intenso de ![]() = 70 sobre la imagen Bárbara. Puede observarse que el método Neigh Shrink no remueve totalmente el ruido y en NeighPreserve aparecen artefactos ajenos a la imagen que se deben a efectos de naturaleza similar al fenómeno de Gibbs. En todos los casos ocurre una inevitable suavización de la imagen. Las estimaciones de mayor calidad visual se obtienen con BiShrink y con el método que se propone.
= 70 sobre la imagen Bárbara. Puede observarse que el método Neigh Shrink no remueve totalmente el ruido y en NeighPreserve aparecen artefactos ajenos a la imagen que se deben a efectos de naturaleza similar al fenómeno de Gibbs. En todos los casos ocurre una inevitable suavización de la imagen. Las estimaciones de mayor calidad visual se obtienen con BiShrink y con el método que se propone.
CONCLUSIONES
Los resultados experimentales arrojan que el método propuesto mejora significativamente a NeighShrink y a NeighPreserve, incrementando, como promedio, en 2 dB el PSNR de la imagen cuando el ruido es intenso. Este incremento se corresponde con una reducción del error medio cuadrático de casi un 60% lo cual indica que el método propuesto captura en mayor grado la correlación intra-escala que NeighShrink y NeighPreserve. El método mejora también a BiShrink para todos los niveles de ruido, aunque los incrementos en PSNR son mucho más modestos, pero no insignificantes pues equivalen a una reducción promedio de un 2% del error medio cuadrático.
En trabajos futuros se deberían abordar las posibles optimizaciones de este método basadas en la minimización del estimador de riesgo de Stein al igual que la influencia del uso de diferentes filtros wavelets en los resultados experimentales.
REFERENCIAS BIBLIOGRÁFICAS
BISWAS M., OM H., A New Adaptive Image Denoising Method Based on Neighboring Coefficients. J. Inst. Eng. India Ser. B, 2016 (January–March) 97(1):11–19
CAI, T. T., SILVERMAN, W., Incorporing information on neighbouring coefficients. Sankhya: The Indian Journal of Statistics, 2001, 63, 127–148.
CHANG, S. G., YU, B., VETTERLI, M., Adaptive wavelet thresholding for image denoising and compression. IEEE Transactions on Image Processing, 2000, 9 (9), 1532–1546.
CHEN G.Y., BUIAND T.D., KRZYZAK A. Image denoising with neighbour dependency and customized wavelet and threshold, Pattern Recognition, 2005, 38, 115-124.
CHO D., BUI T.D., Multivariate statistical modeling for image denoising using wavelet transforms, Signal Processing: Image Communication, 2005, 20 pp.77–89.
DENGWEN Z., WENGANG C., Image denoising with an optimal threshold and neighbouring window. Pattern Recognition Letters 2008, 29 pp. 1694–1697.
DIXIT A., SHARMA P., A Comparative Study of Wavelet Thresholding for Image Denoising. I.J. Image, Graphics and Signal Processing, 2014, 12, pp. 39-46.
DONOHO, D.L., JOHNSTONE, I. M., Ideal spatial adaptation by wavelet shrinkage. Biometrika, 1993, 81, 425–455.
DONOHO, D.L., JOHNSTONE, I. M., Adapting to unknown smoothness via wavelet shrinkage. Journal of the American Statistical Association 1995, 90, 1200–1224.
LEIGH, A., WONG, A., CLAUSI, D. A., FIEGUTH, P., 2011. Comprehensive analysis on the effects of noise estimation strategies on image noise artifact suppression performance. Proceedings of the IEEE International Symposium on Multimedia ISM ’11, 97–104
LIHONG C., ZHAN W., YIGANG C., XUGUANG L., JIANJUN S., An Extension of the Interscale SURE-LET Approach for Image Denoising. International Journal of Advanced Robotic Systems. 2014, 11:9, doi: 10.5772/57294, pp. 1-10.
LIU J., MOULIN P., Information-theoretic analysis of interscale and intrascale dependencies between image wavelet coefficients. IEEE Trans. On Image Processing, 2001, 10(11), 1647-1658.
LUISIER F., The SURE-LET Approach to Image Denoising, Tesis de doctorado, Escuela Politécnica Federal de Lausana, 2010
SABAHALDIN H., GORASHI S., An Efficient Implementation of Neighborhood based Wavelet Thresholding for Image Denoising, International Journal of Computer Applications, 2012, Volume 41– No.9, March.
SENDUR L, SELESNICK I. W., Bivariate Shrinkage with Local Variance Estimation, IEEE Signal Processing Letters, 2002, v. 9, 12, 438-441
VANITHAMANI R., UMAMAHESWARI G., Speckle Reduction in Ultrasound Images using Neighshrink and Bilateral Filtering. Journal of Computer Science, 2014, vol. 10, Issue 4, pp. 623-631.
WILSON S., THANGAMANI M., KONGUVEL E., Detection of Breast Tumour and Speckle Noise Removal using Bilateral Filter and Bivariate Shrinkage. International Journal of Computer Applications, 2015, Volume 116 – No. 3, April.
YANG Y., WEI Y., Neighboring coefficients preservation for signal denoising. Circuits Syst Signal Process, 2012, vol. 31, pp. 827–832.
YANG Y., WEI Y., YANG. M., Signal Denoising Based on the Adaptive Shrinkage Function and Neighborhood characteristics, Circuits Syst Signal Process, 2014, vol. 33, pp. 3921–3930.
Recibido: 12/07/2016
Aceptado: 28/02/2017