My SciELO
Services on Demand
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista Cubana de Ciencias Informáticas
On-line version ISSN 2227-1899
Rev cuba cienc informat vol.12 no.3 La Habana July.-Sept. 2018
ARTÍCULO ORIGINAL
Metric Learning to improve the persistent homology-based gait recognition
Aprendizaje de métrica para mejorar el reconocimiento del andar basado en la homología persistente
Guillermo Aguirre Carrazana1*, Javier Lamar-Leon2, Yenisel Plasencia Calaña2
1Facultad de Matemática y Computación, Universidad de la Habana, San Lázaro y L, Vedado, Habana 4,CP-10400, Cuba. kaprekar.aguirre@gmail.com
2Centro de Aplicaciones de Tecnologías Avanzadas (CENATAV), 7a ] 21812 e/ 218 y 222, Rpto. Siboney, Playa, C.P. 12200, La Habana, Cuba. {jlamar, yplasencia}@centav.co.cu
*Autor para la correspondencia: kaprekar.aguirre@gmail.com
ABSTRACT
Gait recognition is an important biometric technique for video surveillance tasks, due to the advantage of using it at distance. In this paper, we present a persistent homology-based method to extract topological features from the body silhouettes of a gait sequence. It has been used before in several papers for the second author for human identification, gender classification, carried object detection and monitoring human activities at distance. As the previous work, we apply persistent homology to extract topological features from the lowest fourth part of the body silhouette to decrease the negative effects of variations unrelated to the gait in the upper body part. The novelty of this paper is the introduction of the use of a metric learning to learn a Mahalanobis distance metric to robust gait recognition, where we use Linear Discriminant Analysis. This learned metric enforces objects for the same class to be closer while objects from different classes are pulled apart. We evaluate our approach using the CASIA-B dataset and we show the effectiveness of the methods proposed compared with other state-of-the-art methods.
Key words: TDA, gait recognition, persistent homology, linear discriminant analysis, metric learning.
RESUMEN
El reconocimiento del andar es una técnica biométrica importante para las tareas de videovigilancia, debido a la ventaja de su uso a grandes distancias. En este artículo, presentamos un método basado en la homología persistente para extraer características topológicas de las siluetas de una secuencia del andar. Esta metodología ha sido utilizada anteriormente en varios artículos por el segundo autor para la identificación de personas por la forma de caminar, clasificación de género, detección de objetos que transporta la persona y el monitoreo de actividades humanas a una distancia determinada. Como en los trabajos anteriores, aplicamos la homología persistente para extraer las características topológicas de la cuarta parte inferior de la silueta del cuerpo humano con el objetivo de disminuir los efectos negativos de las variaciones no relacionadas con el andar en la parte superior del cuerpo. La novedad de este trabajo es la introducción del uso de un aprendizaje de métrica para el reconocimiento robusto del andar, donde se utiliza la técnica Análisis Discriminante lineal(LDA). Esta métrica aprendida obliga a que los objetos de la misma clase estén más cerca, mientras que los objetos de diferentes clases se separan. Evaluamos nuestro enfoque utilizando la base de datos CASIA-B y mostramos la efectividad de los métodos propuestos en comparación con el estado del arte.
Palabras clave: TDA, reconocimiento de la marcha, homología persistente, análisis de discriminante lineal, aprendizaje de métrica.
INTRODUCTION
Gait is a behavioral biometric which has advantages over other biometrics techniques because it is available even when the subject is at a distance from a camera because it can be recognized from a relatively low-resolution image sequence [Mori et al. (2010)] and the gait features can be obtained without subject cooperation. Because of these advantages, gait recognition is suitable for many applications such as surveillance, forensics, and criminal investigation. Currently, there are good results in the state of the art for persons walking under natural conditions [Yu et al. (2006), Lee et al. (2014), Lamar-Leon et al. (2017)]. However, it is not common for people to walk without carrying a bag, wearing a coat or anything that changes the natural gait. The most successful approaches in gait recognition use silhouettes-based technique to get the features and the best results have been obtained from the methods based in Gait Energy Images (GEI) [Yu et al. (2006), Lee et al. (2014), Rida et al. (2016),Wu et al. (2017)]. The GEI methods have been used to eliminate the effects of carrying a bag or wearing a coat. Moreover, these methods are highly correlated with errors frequently appear in the existing algorithms for background segmentation. This implies that GEI methods are influenced by the shape of the silhouette instead of the relative positions among the parts of the body while walking.
In this work, the gait was modeled using a persistent-homology-based representation (called topological signature of the gait sequence) [Lamar-Leon et al. (2017)], since it gives features of the objects that are invariant to deformation. We start the procedure with a sequence of silhouettes obtained from a video. A simplicial complex ∂K(I) which represents the human gait is then constructed (see Section). Sixteen persistence barcodes are then computed (see Section) considering, respectively, the distance to eight fixed planes (2 horizontals, 2 verticals, 2 oblique and 2 depth planes) in order to completely capture the movement in the gait sequence. To decrease the negative effects of variations unrelated to the gait in the upper body part, we only select the lowest fourth part of the body silhouette (legs-silhouette), (see in Section).
Some researchers have shown that the classification can be further improved by metric learning methods, which are important for many practical applications, such as image retrieval [Lee et al. (2008), Mensink et al. (2013), Gao et al. (2014)], face verification [ Lu et al. (2015), Huang et al. (2015),Koestinger et al. (2012)], and person identification [Chen et al. (2015), Liao et al. (2015), Liao and Li (2015)]. Similarity metric learning aims to learn an appropriate distance or similarity measure to compare pairs of example. This provide a natural solution for the verification task. The most popular way to gain robustness to covariates is to incorporate spatial metric learning based in Mahalanobis distance. However, difficult to cover all the variations only by spatial metric learning because the topological features are affected by covariates such as clothing and carrying bag.
In this work we considered the Linear Discriminant Analysis(LDA) [Hastie and Tibshirani (1996)] to separate pairs of the same subjects and different subjects well in a data-driven way (see in Section). In the context of metric learning, LDA computes a linear projection L that maximizes the amount of between-class variance relative to the amount of within-class variance. Experiments were conducted on CASIA-B gait database and the results in Section demonstrate the improvement of gait recognition performance via the combination of topological features and metric learning.
RELATED WORKS
Gait Recognition overview
In recent years, various techniques have been proposed to solve the gait recognition problem. The appearancebased approaches directly use input or silhouette images in a holistic way to extract gait features without model fitting, and hence they generally work well. In particular, silhouette based representation such as gait energy images(GEI)[Man and Bhanu (2006)], frequency domain features (FDFs)[Makihara et al. (2006)], chrono gait images[Tao et al. (2007)], and Gabor GEIs[Wang et al. (2012)], are dominant in the gait recognition community because of their sample yet effective properties. The appearance-based approaches, however, often suffer from large intra-subject appearance changes due to covariates such as clothing, carrying status, view and walking speed. Model-based methods attempt to explicitly model the human body or motion by employing the static and dynamic body parameters to execute model matching in each frame of a walking sequence. They require a relatively high image resolution to get reasonable human model fitting results and incur high computational costs [Zhao et al. (2006),Ariyanto and Nixon (2011),Bodor et al. (2009)].
Distance metric learning
Euclidean distance is usually used for simplicity, however, it has serious effects on the performance in classification, clustering and retrieval task. Many machine learning methods heavily rely on the selected distance metric, which measures how similar two samples are. Therefore, distance metric leaning has attracted great interest. Most of the distance metric learning algorithms explored the pairwise constrains between training samples to keep the samples of the same class close and the samples from different classes apart.
The distance metrics are based on multivariate data distributions, such as Mahalanobis distance. The most classical algorithm is Xing’s method [Xing et al. (2003)] which formulated distance metric learning as a constrained convex programming problem. Du and Zhang (2014) proposed a Mahalanobis distance based metric learning based on a gradient descent solver with an alternative updating strategy for the purpose of maximizing the inter-class distance, and at the same time minimizing the intra-class distance. Another important family is embedding method, i.e to transform the data set from the original space into its subspace. The most popular way to gain robustness to covariates is to incorporate spatial metric learning such as Linear Discriminant Analysis (LDA) [Hastie and Tibshirani (1996)], general tensor discriminant analysis (GTDA) [Tao et al. (2006)], discriminant analysis with tensor representation (DATER) [Xu et al. (2006)], the random subspace method (RSM) [Guan et al. (2012)]. Zhang et al. (2009) proposed a patch alignment framework to unify PCA, LDA, LPP, NPE and so on, and this work plays an important role in better understanding the intrinsic difference of these manifold leaning based dimension reduction algorithms. Gui et al. (2010) added discriminant information into LPP. Gong et al. (2015) proposed deformed graph Laplacian and signed Laplacian embedding for semi-supervised learning. In contrast to previous metric learning approaches, Gui et al. (2012) proposed a discriminant sparse NPE and later Yang et al. (2015) gave a collaborative representation based on L2 norm graph. In order to improve the discrimination power, Zhou et al. (2011) proposed Simultaneous Discriminant Analysis (SDA) to gather the LR and HR images from the same class and simultaneously separate different classes. Makihara et al. introduce a metric on joint intensity to mitigate the large intra-subject differences and leverage the subtle inter-subject differences. They learn such a metric so as to separate pairs of the same subjects and different subjects well in a data driven way.
Topological model of the gait: Simplicial Complexes
In this section we introduce the construction of the simplicial complexes ∂K(I) which represents the input human gait sequence. We start the procedure with sequence of silhouettes obtained from a gait sequence. With the intention of a fair comparison, we get the sequences from the background segmentation provided in CASIA-B dataset. Figure 1
As we did in previous paper[ Lamar-León et al. (2012), Leon et al. (2013) Lamar-Leon et al. (2014), Lamar-Leon et al. (2016)], for obtaining the simplicial complex from a gait, we first build a 3D binary image I = (Z3,B) by stacking k consecutive silhouettes, where B ⊂ Z3 is the foreground and Bc = Z3 − B is the background, respectively of a subsequence of representation is built stacking silhouettes aligned by their gravity centers (gc). Later, I is used to derive a cubical complex Q(I). The cubical complex is a combinatorial structure constituted by a set of unit cubes with faces parallel to the coordinate planes and vertices in Z3, together with all its faces. The 0−faces of a cube c are its 8 corners (vertices), its 1−faces are its 12 edges, its 2−faces are its 6 squares and, finally, its 3−faces is the cube itself. Then, a cube with vertices V = {(i,j,k),(i+1,j,k),(i,j+ 1,k),(i,j,k+1),(i+1,j +1,k),(i+1,j,k+1),(i,j +1,k+1),(i+1,j +1,k+1)}, with (i,j,k) ∈ Z3, is added to Q(I) together with all its faces if and only V ⊆ B. The simplicial representation ∂K(I) of I is obtained from Q(I) by subdividing each square of Q(I) in 2 triangles together with all their faces (vertices and edges). Finally, coordinates of the vertices of ∂K(I) are normalized to coordinates (x,y,t), where 0 ≤ x,y ≤ 1 and t is the number of silhouette of the sub-sequence of representation.
To decrease the negative effects of variations unrelated to the gait in the upper body start (related, for example, to hand gestures like talking on cell), we selected the lowest fourth part of the body silhouette (legs-silhouette). This selection is endorsed by the result given in [Bashir et al. (2010)] , which shows that this part of the body provides most of the necessary information for classification. We start the procedure with a sequence of silhouettes obtained from a video. With the intention of a fair comparison, we get the sequences from the background segmentation provided in CASIA-B dataset. Figure 2
Filtration of the Simplicial Complex
The next step in this process is to sort the simplices of ∂K(I) in order to obtain a filtration, which is a partial ordering of the simplices of ∂K(I) dictated by a filter function f : ∂K(I) → R, satisfying that if a simplex σ is a face of another simplex σ0 in ∂K(I) then f(σ) ≤ f(σ0) (i.e., σ appears before or at the same time thatσ0 in the ordering). Figura 3
In this work, we use eight filtrations obtained from eight planes. For each plane π, it defines the filter function fπ: ∂K(I) → R which assigns to each vector vertex of ∂K(I) its distance to the plane π, and to any other simplex of ∂K(I), the biggest distance of its vertices to π. Ordering the simplices of ∂K(I) according to the values of fπ, we obtain the filtration ∂Kπ for ∂K(I) associated to the plane π.
Observe that, the filtration associated to each plane is obtained in a different way: By adding one simplex at each time (i.e., a total ordering of the simplices is constructed). Nevertheless, the filtration presented in [Lamar-Leon et al. (2016)] and in this paper, is constructed by adding a bunch of simplices with possible different cardinalities, which makes the method robust to variation in the amount of simplices of the simplicial complex and therefore, robust to noise.
Persistent homology and topological signature
The topological signature of a gait sequence is obtained by the compute the persistent homology of each filtration. Persistent homology is an algebraic tool for measuring topological features of shapes and functions. It is built on top of homology, which is a topological invariant that captures the amount of connected components (0−cycles), tunnels (1−cycles), cavities (2−cycles) and similar in higher dimensions of a shape. Small size features in persistent homology are often categorized as noise, while large size features describe topological properties of shapes [Edelsbrunner and Harer (2010)].
Formally, let K be a simplicial complex. A p−chain is denoted by a Cp(K). Let us define the homomorphism: ∂p : Cp(K) → Cp−1(K) called boundary operator such that for each p−simplex σ of K, ∂p(σ) is the sum of its faces. For example, if σ is a triangle, ∂2(σ) is the sum of its edges. The kernel of ∂p+1 is called the group of p−cycles in Cp(K) and the image of ∂p+1 is called the group of p−boundaries in Cp(K). The p−homology Hp(K) of K is the quotient group of p−cycles relative to p−boundaries. Then, 0−homology classes represents the connected components of K, 1−homology classes its tunnels and 2−homology classes its cavities.
To explain the concept of persistent homology, consider a filtration (i.e., a list of sorted simplices) Kp = (σ1,σ2,··· ,σm) for a simplicial complex K obtained from a given filter function fp : K → R. Suppose that the simplices of the filtration are added in order (i.e., exactly one simplex is added each time). If σi completes a q−cycle (q is the dimension of σi) when σi is added to Ki−1 = (σ1,··· ,σi−1), then a q−homology class γ is born at time fp(σi); otherwise, a (q−1)−homology class dies at time fp(σi). The differences between the birth and death time of a homology class is called its persistence, which quantifies the significance of a topological attribute. If γ never dies, we set its persistence to infinity. For a q−homology class that is born at time fp(σi) and dies at time fp(σj), we draw a segment with endpoints fp(σi) and fp(σj) to get the q−persistence barcode of the filtration.
Topological Signature for a Gait Sequence
Now, the topological signature is computed from the persistence barcodes obtained for ∂Kπ for each plane π.
Observe that fixed a reference plane π, the length of each interval in the persistence barcode obtained for ∂Kπ is: a) less or equal than 1 if π is a horizontal or vertical plane, and b) less or equal than √2 if π is an oblique plane. Now for computing the topological signature, for each plane π, the 0−persistence barcode (i.e., the lifetime of connected components) and the 1−persistence barcode (i.e., the lifetime of tunnels) of the filtration ∂Kpi are explored according to a uniform sampling. More precisely, given a positive integer n (being n = 24 in our experimental results, obtained by cross validation), we computer the integer ![]() which represents the width of the ”window” we use to analyze the persistence barcode, being k the biggest distance of a vertex in ∂K(I) to the given plane π.
which represents the width of the ”window” we use to analyze the persistence barcode, being k the biggest distance of a vertex in ∂K(I) to the given plane π.
For example, let us suppose an scenario in which m j-homology classes are born in [s·h,(s+1)·h] and persist or die at the end of [(s+1)·h,(s+2)·h] and not any other j-homology class is born, persists or dies in these intervals. Then, we put 0 in entries 2s and 2s + 3, and m in entries 2s + 1 and 2s + 2. On the other hand, let us suppose that m j-homology classes are born and die in [s · h,(s + 1) · h] and in [(s + 1) · h,(s + 2) · h] and not any other j-homology class is born, persists or dies in these intervals. Then, we put 0 in entries 2s and 2s + 2 and m in entries 2s + 1 and 2s + 3. Observe that only considering (a) and (b) separately, we can distinguish both scenarios. This way, fixed a plane π, we obtain two 2n-dimensional vectors for Kπ, one for the 0-persistence barcode and the other for the 1-persistence barcode associated to the filtration Kπ. Since we have eight planes, {π1,··· ,π8}, and two vectors per plane, ![]() we have a total of sixteen 2n-dimensional vectors which form the topological signature for a gait sequence.
we have a total of sixteen 2n-dimensional vectors which form the topological signature for a gait sequence.
Metric Learning Approach
Selecting an appropriate distance metric is critical to many learning algorithms, such as k-means, nearest neighbor searches, and others. However, the choice of such a measure is very specific problem and, ultimately dictates the success or failure of the learning algorithm. The distance metric learning approach has been proposed for both unsupervised and supervised problems. In this section, we first introduce the general idea of Mahalanobis metric learning and then give an overview of the approach used in this study.
Mahalanobis distance learning is a prominent and widely approach for improving classification results by exploiting the structure of the data. Given n data points xi ∈ Rm, the goal is to estimate a matrix M such that:
dM(xi,xj) = (xi − xj)T M(xi − xj)
describes a pseudo-metric. In fact, this is assured if M is positive semi-definite. If M = ∑−1(i.e.,the inverse of the sample covariance matrix), then dM is referred to as the Mahalanobis distance. Thus, given a pair pf samples (xi,xj) we break down the original multi-class problem into a two-class problem in two steps. First, we transform the samples from the data space to the label difference space X = {xij = xi − x − j} which is inherently given by the metric definitions. Moreover, X is invariant to the actual locality of the samples in the feature space. Second, the original class labels are discarded and the samples are arranged using pairwise equality and inequality constrains, where obtain the classes same S and different D:
S = {(xi,xj)|y(xi) = y(xj)}
D = {(xi,xj)|y(xi) 6![]() y(xj)}
y(xj)}
In our particular case the pair (xi,xj) consists of the topological descriptor associated to each sample.
Linear Discriminant Analysis: Different ways have been proposed to estimate Mahalanobis distance metrics to compute distance in k-NN classification. This approach has been used to discover informative linear transformations of the input space, which can be seen as inducing a Mahalanobis distance metric in the original space.
Let xi ∈ Rm be a sample and c its corresponding class label. Then, the goal of Linear Discriminant Analysis(LDA) Hastie and Tibshirani (1996) is to compute a classification function g(x) = LT x such that the Fisher-criterion
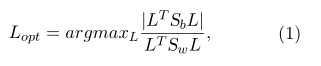
where Sw and Sb are the within-class scatter and between-class scatter matrices, is optimized.
In fact, LDA is to project the high-dimensional samples into a low-dimensional subspace using linear mapping, which has the maximum inter-class distance and minimum intra-class distance between the projected samples in the low dimensional subspace through searching for an optimized projection matrix. It operates in a supervised setting and uses the class labels of the inputs to derive informative linear projections. In the context of metric learning, LDA computes a linear projection L that maximizes the amount of between-class variance relative to the amount of within-class variance. The linear transformation L is chosen to maximize the ratio of between-class to within-class variance, subject to the constraint that L defines a projection matrix. The traditional LDA algorithm is still attractive compared to several recently developed metric learning [Liao et al. (2014)].
RESULTS AND DISCUSSION
In this section we show the results in two experiments using CASIA-B dataset. The CASIA-B dataset has 124 persons, and 10 samples for each of 11 different angles at which a person is taken. For each angle there are six samples walking under natural conditions (CASIA-Bnm), there are two samples of persons carrying some sort of bag (CASIA-Bbg) and the remaining two samples for persons wearing coat (CASIA-Bcl). CASIA-B provides image sequences with background segmentation for each person. In the first experiment we used four sequences by person from the CASIA-Bnm to train and we used the other two sequences by person from CASIA-Bnm, CASIA-Bbg and CASIA-Bcl to test. Our results for side view (90 degrees) are reported in Table 1, where the experiment was repeated 5 times using 200 PCA components, which provide the best results. The result of our previous method using cosine distance and angle distance was also evaluated using always the lowest fourth part of the body silhouette.
In the second experiment, we considered a mixture of normal, carrying-bag and wearing-coat sequences, since it models a more realistic situation where persons do not collaborate while the samples are being taken. We take six sequences to train: four sequences from CASIA-Bnm, one sequence from CASIA-Bbg and one sequence from CASIA-Bcl, the rest was used to test. Using this training data we generated 123 topological signatures, one for each person in the database, this gave us 246 sequences for testing: 123 persons times 2 sequences by person. The experiment was repeated 5 times using 200 PCA components too. Table 2 shows the result of the accuracy. As it can be seen in tables, in general to introduce a metric learning to replace the cosine and angle distance achieve better results.
CONCLUSIONS
In this paper we have presented an algorithm for gait recognition, a technique with special attention in tasks of video surveillance. We have used persistent homology to model the gait, similar, as we did in our previous approaches. The algorithm presented here is slightly different to previous works in the final step (classification), where, we introduced the use of metric learning to learn a Mahalanobis distance metric to robust gait recognition. This learned metric enforces objects for the same class to be closer while objects from different classes are pulled apart. We conducted experiments using CASIA-B database, and showed the effectiveness of the methods proposed compared with other state-of-the-art methods. Besides, the topological features have been tested here using only the lowest fourth part of the body silhouette. Then, the effects of variations unrelated to the gait in the upper body part, which are very frequent in real scenarios, decrease considerably. This confirms that the highest information in the gait is in the motion of the legs and to learn the similarity from data improves the results.
REFERENCES
Gunawan Ariyanto and Mark S Nixon. Model-based 3d gait biometrics. In Biometrics (IJCB), 2011 International Joint Conference on, pages 1–7. IEEE, 2011.
Khalid Bashir, Tao Xiang, and Shaogang Gong. Gait recognition without subject cooperation. Pattern Recognition Letters, 31(13):2052–2060, 2010.
Robert Bodor, Andrew Drenner, Duc Fehr, Osama Masoud, and Nikolaos Papanikolopoulos. View-independent human motion classification using image-based reconstruction. Image and Vision Computing, 27(8):1194– 1206, 2009.
Dapeng Chen, Zejian Yuan, Gang Hua, Nanning Zheng, and Jingdong Wang. Similarity learning on an explicit polynomial kernel feature map for person re-identification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 1565–1573, 2015.
Bo Du and Liangpei Zhang. A discriminative metric learning based anomaly detection method. IEEE Transactions on Geoscience and Remote Sensing, 52(11):6844–6857, 2014.
Herbert Edelsbrunner and John Harer. Computational topology: an introduction. American Mathematical Soc., 2010.
Xingyu Gao, Steven CH Hoi, Yongdong Zhang, Ji Wan, and Jintao Li. Soml: Sparse online metric learning with application to image retrieval. In AAAI, pages 1206–1212, 2014.
Chen Gong, Tongliang Liu, Dacheng Tao, Keren Fu, Enmei Tu, and Jie Yang. Deformed graph laplacian for semisupervised learning. IEEE transactions on neural networks and learning systems, 26(10):2261–2274, 2015.
Yu Guan, Chang-Tsun Li, and Yongjian Hu. Robust clothing-invariant gait recognition. In Intelligent Information Hiding and Multimedia Signal Processing (IIH-MSP), 2012 Eighth International Conference on, pages 321–324. IEEE, 2012.
Jie Gui, Wei Jia, Ling Zhu, Shu-Ling Wang, and De-Shuang Huang. Locality preserving discriminant projections for face and palmprint recognition. Neurocomputing, 73(13):2696–2707, 2010.
Jie Gui, Zhenan Sun, Wei Jia, Rongxiang Hu, Yingke Lei, and Shuiwang Ji. Discriminant sparse neighborhood preserving embedding for face recognition. Pattern Recognition, 45(8):2884–2893, 2012.
Trevor Hastie and Robert Tibshirani. Discriminant adaptive nearest neighbor classification. IEEE transactions on pattern analysis and machine intelligence, 18(6):607–616, 1996.
Zhiwu Huang, Ruiping Wang, Shiguang Shan, and Xilin Chen. Face recognition on large-scale video in the wild with hybrid euclidean-and-riemannian metric learning. Pattern Recognition, 48(10):3113–3124, 2015.
Martin Koestinger, Martin Hirzer, Paul Wohlhart, Peter M Roth, and Horst Bischof. Large scale metric learning from equivalence constraints. In Computer Vision and Pattern Recognition (CVPR), 2012 IEEE Conference on, pages 2288–2295. IEEE, 2012.
J Lamar-Leon, Raul Alonso-Baryolo, Edel Garcia-Reyes, and R Gonzalez-Diaz. Persistent-homology-based gait recognition. arXiv preprint arXiv:1707.06982, 2017.
Javier Lamar-León, Edel B Garcia-Reyes, and Rocio Gonzalez-Diaz. Human gait identification using persistent homology. In Iberoamerican Congress on Pattern Recognition, pages 244–251. Springer, 2012.
Javier Lamar-Leon, Raul Alonso Baryolo, Edel Garcia-Reyes, and Rocio Gonzalez-Diaz. Gait-based carried object detection using persistent homology. In Iberoamerican Congress on Pattern Recognition, pages 836– 843. Springer, 2014.
Javier Lamar-Leon, Raul Alonso-Baryolo, Edel Garcia-Reyes, and Rocio Gonzalez-Diaz. Persistent homologybased gait recognition robust to upper body variations. In Pattern Recognition (ICPR), 2016 23rd International Conference on, pages 1083–1088. IEEE, 2016.
Chin Poo Lee, Alan WC Tan, and Shing Chiang Tan. Time-sliced averaged motion history image for gait recognition. Journal of Visual Communication and Image Representation, 25(5):822–826, 2014.
Jung-Eun Lee, Rong Jin, and Anil K Jain. Rank-based distance metric learning: An application to image retrieval. In Computer Vision and Pattern Recognition, 2008. CVPR 2008. IEEE Conference on, pages 1–8. IEEE, 2008.
Javier Lamar Leon, Andrea Cerri, Edel Garcia Reyes, and Rocio Gonzalez Diaz. Gait-based gender classification using persistent homology. In Iberoamerican Congress on Pattern Recognition, pages 366–373. Springer, 2013.
Shengcai Liao and Stan Z Li. Efficient psd constrained asymmetric metric learning for person re-identification. In Proceedings of the IEEE International Conference on Computer Vision, pages 3685–3693, 2015.
Shengcai Liao, Zhen Lei, Dong Yi, and Stan Z Li. A benchmark study of large-scale unconstrained face recognition. In Biometrics (IJCB), 2014 IEEE International Joint Conference on, pages 1–8. IEEE, 2014.
Shengcai Liao, Yang Hu, Xiangyu Zhu, and Stan Z Li. Person re-identification by local maximal occurrence representation and metric learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2197–2206, 2015.
Ait O Lishani, Larbi Boubchir, and Ahmed Bouridane. Haralick features for gei-based human gait recognition. In Microelectronics (ICM), 2014 26th International Conference on, pages 36–39. IEEE, 2014.
Jiwen Lu, Gang Wang, Weihong Deng, and Kui Jia. Reconstruction-based metric learning for unconstrained face verification. IEEE Transactions on Information Forensics and Security, 10(1):79–89, 2015.
Yasushi Makihara, Atsuyuki Suzuki, Daigo Muramatsu, Xiang Li, and Yasushi Yagi. Joint intensity and spatial metric learning for robust gait recognition.
Yasushi Makihara, Ryusuke Sagawa, Yasuhiro Mukaigawa, Tomio Echigo, and Yasushi Yagi. Gait recognition using a view transformation model in the frequency domain. Computer Vision–ECCV 2006, pages 151–163, 2006.
Ju Man and Bir Bhanu. Individual recognition using gait energy image. IEEE transactions on pattern analysis and machine intelligence, 28(2):316–322, 2006.
Thomas Mensink, Jakob Verbeek, Florent Perronnin, and Gabriela Csurka. Distance-based image classification: Generalizing to new classes at near-zero cost. IEEE transactions on pattern analysis and machine intelligence, 35(11):2624–2637, 2013.
Atsushi Mori, Yasushi Makihara, and Yasushi Yagi. Gait recognition using period-based phase synchronization for low frame-rate videos. In Pattern Recognition (ICPR), 2010 20th International Conference on, pages 2194–2197. IEEE, 2010.
Imad Rida, Somaya Almaadeed, and Ahmed Bouridane. Gait recognition based on modified phase-only correlation. Signal, Image and Video Processing, 10(3):463–470, 2016.
Shamsher Singh and KK Biswas. Biometric gait recognition with carrying and clothing variants. In International Conference on Pattern Recognition and Machine Intelligence, pages 446–451. Springer, 2009.
Dacheng Tao, Xuelong Li, Stephen J Maybank, and Xindong Wu. Human carrying status in visual surveillance. In Computer Vision and Pattern Recognition, 2006 IEEE Computer Society Conference on, volume 2, pages 1670–1677. IEEE, 2006.
Dacheng Tao, Xuelong Li, Xindong Wu, and Stephen J Maybank. General tensor discriminant analysis and gabor features for gait recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 29 (10), 2007.
Chen Wang, Junping Zhang, Liang Wang, Jian Pu, and Xiaoru Yuan. Human identification using temporal information preserving gait template. IEEE Transactions on Pattern Analysis and Machine Intelligence, 34 (11):2164–2176, 2012.
Zifeng Wu, Yongzhen Huang, Liang Wang, Xiaogang Wang, and Tieniu Tan. A comprehensive study on crossview gait based human identification with deep cnns. IEEE transactions on pattern analysis and machine intelligence, 39(2):209–226, 2017.
Eric P Xing, Michael I Jordan, Stuart J Russell, and Andrew Y Ng. Distance metric learning with application to clustering with side-information. In Advances in neural information processing systems, pages 521–528, 2003.
Dong Xu, Shuicheng Yan, Dacheng Tao, Lei Zhang, Xuelong Li, and Hong-Jiang Zhang. Human gait recognition with matrix representation. IEEE Transactions on Circuits and Systems for Video Technology, 16(7): 896–903, 2006.
Wankou Yang, Zhenyu Wang, and Changyin Sun. A collaborative representation based projections method for feature extraction. Pattern Recognition, 48(1):20–27, 2015.
Shiqi Yu, Daoliang Tan, and Tieniu Tan. A framework for evaluating the effect of view angle, clothing and carrying condition on gait recognition. In Pattern Recognition, 2006. ICPR 2006. 18th International Conference on, volume 4, pages 441–444. IEEE, 2006.
Tianhao Zhang, Dacheng Tao, Xuelong Li, and Jie Yang. Patch alignment for dimensionality reduction. IEEE Transactions on Knowledge and Data Engineering, 21(9):1299–1313, 2009.
Guoying Zhao, Guoyi Liu, Hua Li, and Matti Pietikainen. 3d gait recognition using multiple cameras. In Automatic Face and Gesture Recognition, 2006. FGR 2006. 7th International Conference on, pages 529– 534. IEEE, 2006.
Changtao Zhou, Zhiwei Zhang, Dong Yi, Zhen Lei, and Stan Z Li. Low-resolution face recognition via simultaneous discriminant analysis. In Biometrics (IJCB), 2011 International Joint Conference on, pages 1–6. IEEE, 2011.
Recibido: 30/11/2017
Aceptado: 16/05/2018














