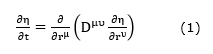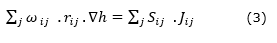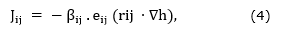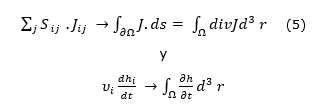Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Ciencias Forestales
versión On-line ISSN 2310-3469
Rev cubana ciencias forestales vol.8 no.3 Pinar del Río sept.-dic. 2020 Epub 06-Sep-2020
Original article
Movement of water in the wood during drying discreet model
1Universidad de Pinar del Río "Hermanos Saíz Montes de Oca". Pinar del Río, Cuba.
2Universidad Católica del Norte. Antofagasta. Chile.
The knowledge of the factors that produce the deformations of the wood can help to a suitable selection of the material before its sawing. One way to address the problem of deformation is with the understanding of the mechanisms that regulate it. The objective of the work was to describe the behavior of the movement of water during the drying of wood as an influential factor in the deformations of the same during this process from a theoretical model, which unifica features Newton's dynamics of a system of particles and schemes of the methods of the finite elements. This model allows to establish in detail the qualitative and quantitative influence of the humidity in the nature of the deformations, which facilitates to value the experimental results, to make predictions in the practical activity, and to obtain a considerable saving of resources and time.
Key words: Moisture; Wood; Drying; Model.
Introduction
The consumption of large volumes of sawn wood in our country indicates as a fundamental need to increase the efficiency of the sawing industry, taking into account to minimize the contractions and other deformations that it presents after its drying, because in the construction the deformations that the sawn wood experiences affect its quality, being the most important property the swelling and the contraction (Álvarez et al., 2013).
Contraction occurs only when the wood loses humidity below the saturation point of the ûbra (PSF). This point is an interesting fact for the structural and decorative uses of wood. It is accepted that for the practical use of all species the average value of the fibre saturation point is 30 %. (Álvarez et al., 2013). As a result of the movement of water during the drying process, the wood undergoes changes in its physical and mechanical properties (Sokolowskyy et al., 2014).
The bound water is attached to the cell walls by very intense physical and chemical forces. During the drying process, first all the free water is removed and then some of the bound water is removed. The removal of the free water is carried out quickly and the energy consumption is relatively low, as the free water is very weakly bound to the wood. The wood begins to lose water until it reaches a point called: Fiber Saturation Point (FSP) in which it no longer has free water to lose. During this phase there are no dimensional changes in the wood, because the water that was inside the cells has been eliminated (Álvarez et al., 2013).
Associated to the humidity changes there are deformations of the wood of Pinus caribaea var. caribaea(González-Cruz, 2008 and Guera et al., 2020). According to Sokolowskyy et al., (2014), the application of mathematical modeling makes it possible to automate the analysis of the phenomena that occur during the drying process.
Different mathematical methods have been used to define the movement of water in the wood during drying, among which the works developed by (Salinas et al., 2010 and Salinas et al., 2015), Pérez et al. (2018), Montero et al. (2020).
The treatment of deformations associated with humidity gradients during the drying process is traditionally described from a theoretical point of view using the Theory of Continuous Media (Ormarsson et al., 2000). This working model, which considers the anisotropy and non-homogeneity of the medium, offers valuable results in the treatment of this phenomenon (deformations) but for its assumptions leaves out of reach the consideration of the discontinuous properties that are inherent to a medium as exceptional as wood (González-Cruz, 2008).
A different vision is proposed in this work: The study of the movement of water in wood during drying, using discrete models that make use of the Newtonian formulation of particle systems, which are widely used in physics to study the behavior of gases, liquids and solids using the methods of classical molecular dynamics. There is a significant knowledge of the peculiarities that these models allow to describe. To gain a better understanding of this phenomenon, a theoretical study of the movement of water during the drying process of the sawn wood of Pinus caribaea Morelet var. caribaea.
The objective of this study is to describe the behavior of the movement of water in the sawn wood of Pinus caribaea Morelet var. caribaea from the theoretical model. This description provides important elements for the area of wood technology and the sawing industry (González-Cruz et al., 2007; González-Cruz, 2008; Montero et al., 2020), who considers that simulation is widely used to improve and optimize the drying process of wood.
Materials and methods
The basic idea of the discrete model starts from considering a portion of the material in small non-overlapping volumes or cells as done in the finite element methods. This portion should be represented schematically (Figure 1) by a grid in which each node is equivalent to a given elementary volume of the material studied, which are linked by segments or links, representing the contact surfaces between adjacent cells. These nodes will have associated the physical properties that we describe in this case: the position radius vector (ri) of the i-ésimo node will represent from now on the position of its center of mass, to which is also associated the mass (mi), volume (Vi) or humidity content h (hi).
The links form the basis of the dynamic mechanism by which the nodes interact by modifying the humidity during the diffusion process that takes place during drying.

Fig. 1. - Discrete recreation of a piece of sawn wood in which only two species of nodes have been considered (marked with different colors), modeling what will be the characteristic ring structure of this material
In order to have a dense representation of the nodes/cells to establish the reticular model of a piece of sawn wood, a grid formed by parallel planes in the shape of a regular triangular net was used. Each node of this network has 12 close neighboring nodes, whose links with the first one defines the directions of application of the interactions and of water transport (diffusion) during the drying process.
To study the dynamics of water during drying, we assume pieces of sawn wood with sections of (10×10×100) mm, which were recreated in the discrete model by a grid formed by 10×11×100 = 11000 nodes.
Movement of bound water
This study is limited to the dynamics of bound water under the assumption that the initial state of the samples is close to the saturation point of the ûbra. In this case, the drying process of bound water takes place through a diffusion process (Gatica et al., 2011; Montero et al., 2020) which can be described in general by the (Equation 1).
D µu - Diffusion tensor (non-homogeneous, anisotropic)
Reformulation of the diffusion in terms of the discrete model
The reformulation of the equations associated with the diffusion process in the continuous medium to the frame of the discrete model is established by assuming that the speed of change of the bound water content per unit volume in the i-ésimo node (particle) with volume (vi) is subjected to the (Equation 2).
Where ω ij is the probability of transit of bound water through the link ij , which satisfies the relation ω ij = ω ij that guarantees that the contribution of the flujo of bound water coming from the j- ésimo node is equal to the partial loss that this last node has with that link.
This transit probability is assumed to be proportional to the area S ij of the superûcie of contact between adjacent cells associated with the nodes involved in the link Jω ij = S ij .β ij j, where β ij is the transit probability per unit area.
The move to the continuum is made by considering the approximation h j -h i = r ij Vh where the terms from ûujo can be rewritten as follows (Equation 3).
Where S ij = S ij . e ij vector area associated with the link(ij) whose normal vector e ij = r ij /|r ij | is directed along the link in the direction of the j-ésimo node, and j ij (Equation 4).
The resulting ûujo humidity at the link address.
When entering the limit to the continuum (Equation 5) and (Equation 6).
The continuity equation is deduced (6)
There is a general linear relationship between flow and humidity gradient, as expressed by the equation 7 (Equation 7).
The equations that describe this study were implemented computationally through the use of the FORTRAN programming language in order to perform the numerical analysis. The results derived from such studies were analyzed using the ORIGIN 6.0.
To study the influence of the environmental conditions that influence the dynamics of the drying process, the process was analyzed for two drying regimes with different values of humidity content at the border of the sawn pieces: the first for 3 %, corresponding to a low environmental humidity content such as those reached by kiln drying, and the second for 10 %, associated with what would be natural drying, also assumed by Ormarsson et al., (2000).
Results and discussion
In general terms, only theoretical modeling allows to establish in detail the qualitative and quantitative influence of influential factors in the nature of the phenomenon studied, arriving at a deep understanding of it that not only allows to understand and explain experimental results; but also, to predict them.
Comparison between two drying regimes
It should be noted that humidity is a variable that was not experimentally controlled, so the results presented are model predictions derived from the numerical simulation of the phenomenon.
Figure 2 shows the evolution of the drying process of sawn wood pieces in terms of average humidity for the two types of boundary conditions considered in this study. The time scale is referred to in units of the simulation. The horizontal lines indicate the level of humidity content corresponding to the PSF and the values at the borders ηf =0 ,03 (3 %) and 0.10 (10 %) used in the numerical experiments.
The drying process runs faster the lower the ambient humidity, reaching a standard humidity content value of ηprom=0 ,12 (12 %) involves a time two to three times longer, for a humidity content at the edge of the pieces ηf =0 ,10 (10 %) than that involved for when ηf=0 ,03. (3 %). This result is interpreted in a similar way to that obtained by Montero (2020) in the simulation of drying in Eucalyptus nitens using diffusion models.
Humidity behavior with the advance of drying
Figures 3 and 4 show the humidity content distributions for the average humidity values ηprom=0.25 (25 %); 0.18 (18 %); 0.15 (15 %) and 0.12 (12 %) obtained through the numerical simulation of the drying process of the sawn wood pieces. The regions where the humidity content is very close to the PSF are represented in black, with less intense grey representing the lower humidity values (Figure 3) y (Figure 4).

Fig. 3. - Humidity distribution in the cross-section of the workpiece with the drying progress for a humidity content at the border of 3 %
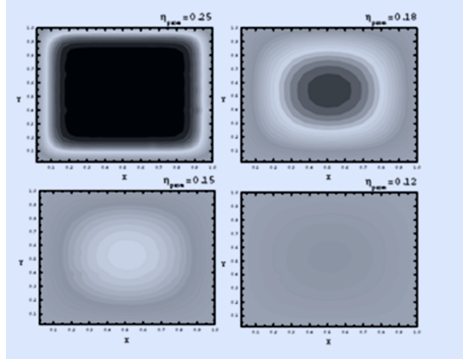
Fig. 4. - Humidity distribution in the cross-section of the workpiece with the drying progress for a humidity content at the border of 10 %
It is interesting to verify the persistence of a central region with a humidity content very close to the saturation point of the fiber even for relatively low average humidity values ~ 0.15 (15%) corresponding to the drying process under low environmental humidity conditions (when ηf= 0.03), results similar to those obtained by Montero (2020).
These results clearly indicate that while the outer regions of the parts tend to shrink due to humidity loss, the central region with humidity close to the PSF is not subject to shrinkage processes, hence stresses associated with these humidity gradients arise between the outer and inner areas, Similar behavior was obtained in the mathematical modeling of conventional drying in European oak Quercus pedonculae wood by Sandoval-Torres, (2009) and in the simulation of stresses during the drying process, considering the variations of moisture in Eucalyptus nitens wood by Pérez et al. (2018).
These tensions may not cause significant deformations in the parts in these states, but they may lead to the formation of cracks and fractures in the sinus and surface of the material when these exceed the limits of resistance of the material, which should be more pronounced as the dimensions of the parts increase.
Although the drying process that takes place under conditions of ambient humidity that are not so low (in our case ηf= 0,10) is slower, it has the advantage of not causing great humidity tensions, since in this the drying occurs more homogeneously in the volume of the pieces, thus avoiding the appearance of high humidity gradients, a behavior that does not favor the appearance of cracks and fractures in the pieces
The greatest deformations should occur once these interior regions with high humidity values have disappeared, and the contractions are present in the entire volume of the pieces.
Conclusions
The theoretical modeling of the drying phenomenon using the discrete model makes it possible to analyze the behavior of the distribution of humidity content during the progress of drying, a study that leads to greater compression of the process.
While the outer regions of the parts tend to shrink due to humidity loss, the central region with humidity close to the PSF is not subject to shrinkage processes, hence tensions arise between the outer and inner areas.
The drying speed is higher for those regimes where the environmental humidity conditions are lower; but this fact has the disadvantage of causing greater humidity gradients between the borders and the interior of the pieces, causing the existence of tensions that can potentially cause cracks and fractures in their borders.
Referencias bibliográficas
GATICA, Y.A., SALINAS, C.H. y ANANIAS, R.A., 2011. MODELING CONVENTIONAL ONE-DIMENSIONAL DRYING OF RADIATA PINE BASED ON THE EFFECTIVE DIFFUSION COEFFICIENT. Latin American Applied Research [en línea], vol. 14, no. 2, pp. 183-189. [Consulta: 20/09/2020]. Disponible en: Disponible en: https://revistas.uns.edu.ar/laar2/article/view/217 . [ Links ]
GONZÁLEZ, I., ÁLVAREZ, D., QUINTERO, A., ALVES, A. y RODRÍGUEZ, J., 2007. Comportamiento de algunas propiedades físicas en la dirección radial de la madera de la especie de Pinus caribaea Morelet var. caribaea. Revista Baracoa [en línea], vol. 2, no. 1. ISSN 0138-6441. Disponible en: https://agris.fao.org/agris-search/search.do?recordID=CU2010800039. [ Links ]
GONZÁLEZ-CRUZ, I., 2008. Análisis de las deformaciones de la madera aserrada de Pinus caribaea Morelet var. caribaea [en línea]. Tesis presentada en opción al grado científico de Doctora en Ciencias Forestales. Pinar del Río, Cuba.: Universidad de Pinar del Río «Hermanos Saíz Montes de Oca». Disponible en: https://agris.fao.org/agris-search/search.do?recordID=CU2011800029. [ Links ]
GUERA, O.G.M., SILVA, J.A.A. da, FERREIRA, R.L.C., ÁLVAREZ LAZO, D., BARRERO MEDEL, H., GUERA, O.G.M., SILVA, J.A.A. da, FERREIRA, R.L.C., ÁLVAREZ LAZO, D. y BARRERO MEDEL, H., 2019. Modelos matemáticos para la determinación del turno óptimo en plantaciones forestales. Madera y bosques, vol. 25, no. 1. . ISSN 1405-0471. DOI 10.21829/myb.2019.2511636. Disponible en: http://www.scielo.org.mx/scielo.php?script=sci_abstract&pid=S1405-04712019000100209&lng=es&nrm=iso&tlng=es. [ Links ]
MONTERO, C., ROZAS, C. y PICANTE, C., 2020. Simulación del secado en madera de Eucalyptus usando modelos de difusión bajo condiciones unidimensionales e isotérmicas. Scientia forestalis [en línea], vol. 48, no. 126. Disponible en: https://www.ipef.br/publicacoes/scientia/nr126/2318-1222-scifor-48-126 -e2957.pdf. [ Links ]
ORMARSSON, S., DAHLBLOM, O. y PETERSSON, H., 2000. A numerical study of the shape stability of sawn timber subjected to moisture variation. En: Company: SpringerDistributor: SpringerInstitution: SpringerLabel: Springernumber: 3publisher: Springer-Verlag, Wood Science and Technology [en línea], vol. 34, no. 3, pp. 207-219. [Consulta: 20/09/2020]. ISSN 1432-5225. DOI 10.1007/s002260000042. Disponible en: Disponible en: https://link.springer.com/article/10.1007/s002260000042 . [ Links ]
PÉREZ-PENA, N., CHÁVEZ, C., SALINAS, C. y ANANÍAS, R.A., 2018. Simulation of Drying Stresses in Eucalyptus nitens Wood. BioResources [en línea], vol. 13, no. 1, pp. 1413-1424. [Consulta: 20/09/2020]. ISSN 1930-2126. Disponible en: Disponible en: https://ojs.cnr.ncsu.edu/index.php/BioRes/article/view /BioRes_13_1_1413_Perez_Pena_Simulation_Drying_Stress_Eucalyptus . [ Links ]
SALINAS, C., ANANIAS, R., GATICA, Y. y CHAVEZ, C., 2010. Simulation of the Dryng Stresses in Wood. Mecánica Computacional [en línea], vol. 29, no. 85, pp. 8347-8354. [Consulta: 20/09/2020]. Disponible en: Disponible en: https://cimec.org.ar/ojs/index.php/mc/article/view/3602 . [ Links ]
SALINAS, C., CHAVEZ, C., ANANIAS, R.A. y ELUSTONDO, D., 2015. Unidimensional Simulation of Drying Stress in Radiata Pine Wood. Drying Technology [en línea], vol. 33, no. 8, pp. 996-1005. [Consulta: 20/09/2020]. ISSN 0737-3937. DOI 10.1080/07373937.2015.1012767. Disponible en: Disponible en: https://doi.org/10.1080/07373937.2015.1012767 . [ Links ]
YURIY, P., IGOR, K. y YAROSLAV, S., 2014. Mathematical modeling of timber elastic-viscous-plastic deformation in the wood drying process. Лесотехнический журнал [en línea], vol. 4, no. 2 [Consulta: 20/09/2020]. ISSN 2222-7962. Disponible en: Disponible en: https://cyberleninka.ru/article/n/mathematical-modeling-of-timber-elastic-viscous-plastic-deformation-in-the-wood-drying-process . [ Links ]
Received: August 20, 2020; Accepted: September 20, 2020











 texto en
texto en